DM spé maths
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 17:15
par moranie » 24 Oct 2007, 17:15
bonjour, j'aurai besoin d'aide pour un exercice de spé maths
il faut démontrer que "n est divisible par 3 si et seulement si n^4 est divisible par 3" sachant d'après les questions précédentes que (n-2)^4 est congru à n^4+n^3+n+1 modulo 3
si et seulement si demande une démonstration dans les deux sens or je n'arrive pas a venir a bout de cette démonstration
merci d'avance pour votre aide
moranie
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Oct 2007, 17:19
par Imod » 24 Oct 2007, 17:19
Les deux questions sont indépendantes , 3 est un nombre premier , dire qu'il divise n ou n^4 est équivalent .
Imod
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 17:30
par moranie » 24 Oct 2007, 17:30
Imod,
...donc dans ce cas là une démonstration n'est pas indispensable??
moranie :hein:
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Oct 2007, 17:33
par Imod » 24 Oct 2007, 17:33
Si quand même !
Dans un sens c'est évident , si 3 divise n il divise n^4 .
La réciproque utilise le théorème de Gauss si 3 ( premier ) divise n.n.n.n alors 3 divise n .
Imod
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 17:53
par moranie » 24 Oct 2007, 17:53
merci,
maintenant un deuxième problème se pose à moi il faut que je determine les entiers n tel quel n^4+n^3+n+1 soit divisible 3
moranie
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Oct 2007, 17:56
par Imod » 24 Oct 2007, 17:56
Commence par factoriser ton expression :
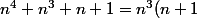+(n+1)=...)
Imod
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 17:59
par moranie » 24 Oct 2007, 17:59
et j'en déduis que la factorisation est congru à 0 modulo 3?
moranie
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Oct 2007, 18:08
par Imod » 24 Oct 2007, 18:08
Oui et le procédé classique , un produit est divisible par 3 si l'un de ses facteurs est divisible par 3 .
Imod
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 18:18
par moranie » 24 Oct 2007, 18:18
je modifie l'expresiion pour avoir deux facteurs
(n+1)(n^3+1)
et il me faut un facteur divisible par 3
donc je prend le plus simple =>n+1
n+1=3k avec kZ
ce qui me donne n=2k
ça peut marcher avec cette méthode
merci de me guider pour cette exercice
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Oct 2007, 18:21
par Imod » 24 Oct 2007, 18:21
moranie a écrit:n+1=3k avec kZ ce qui me donne n=2k
Vraiment sûr :hein:
Imod
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 18:22
par moranie » 24 Oct 2007, 18:22
non
3k-1!
désolé
-
moranie
- Membre Naturel
- Messages: 10
- Enregistré le: 24 Oct 2007, 17:06
-
 par moranie » 24 Oct 2007, 18:23
par moranie » 24 Oct 2007, 18:23
non
3k-1
désolé
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Oct 2007, 18:25
par Imod » 24 Oct 2007, 18:25
C'est à dire

modulo 3 . Je te laisse faire pour le deuxième facteur .
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 135 invités
