Exponentielle complexe

[jean77]

Question bête,

je peux écrire (exp(in )=(exp(i))=(-1)
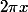
mais pas, par exemple: (exp(i )=(exp(i))=(1)=1 ce qui est de toute évidence faux.
Ne peut on pas manipuler l'exponentille complexe comme l'exponentielle réelle et pourquoi?


Merci de votre aide

[tize]

Bonjour,
la fonction puissance est définie comme ceci :

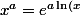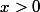
il n'y a donc pas de problème pour mais si est un nombre complexe alors il n'y a pas qu'une seule possibilité pour , cela dépend de la détermination du log choisit...

[kazeriahm]

salut

en fait quand on parle de z^a avec z et a complexes, on a au préalable définit ce qu'était le logarithme complexe

tu peux trouver des infos sur la manière de définir cette fonction sur wikipédia je pense, mais la réponse à ta question vient du fait que si z est complexe, en désignant ppar log le logarithme complexe,

on exp(ln(z))=z mais pas forcément ln(exp(z))=z

[tize]

Tu peux aussi regarder l'énigme 53 de ce site ainsi que la "réponse" qui y est donnée.

[quinto]

on exp(ln(z))=z mais pas forcément ln(exp(z))=z

Attention tout de même puisque le logarithme complexe n'est pas défini pour tout z.

Une formulation plus rigoureuse serait celle ci:
soit un chemin reliant 0 a z, alors
= z pour tout z.