Tableau de variation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
pandatesk
- Messages: 5
- Enregistré le: 29 Aoû 2007, 09:42
-
 par pandatesk » 29 Aoû 2007, 09:49
par pandatesk » 29 Aoû 2007, 09:49
Bonjour à tous ! Pouvez vous m'aider ?
f(x) = 1-2x-4/x
Apres avoir déterminer les limites de f, préciser les asymptotes verticales et rechercher les asymptotes horizontales, puis enfin dériver f, on me demande de : Dresser le tableau de variation complet de f.
Pouvez vous m'aider ? (c'est le mot "complet" qui m'a dérangé)
Merci d'avance !
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 29 Aoû 2007, 09:52
par fonfon » 29 Aoû 2007, 09:52
salut,
le tableau de variation complet c'est juste que tu resumes ds le tableau tout ce que tu as etudié avant variations limites eventuellement les extrema si il y en a
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 29 Aoû 2007, 10:05
par fonfon » 29 Aoû 2007, 10:05
re,
as-tu au moins reussi qq chose?
-
pandatesk
- Messages: 5
- Enregistré le: 29 Aoû 2007, 09:42
-
 par pandatesk » 29 Aoû 2007, 10:09
par pandatesk » 29 Aoû 2007, 10:09
Presque, là je suis en train de dériver mais j'ai un peu de mal
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 29 Aoû 2007, 10:12
par fonfon » 29 Aoû 2007, 10:12
re,
ta fonction c'est bien
}=1-2x-\frac{4}{x})
si c'est le cas ecris que
}=1-2x-4\times\frac{1}{x})
et là tu devrais y arriver
ou au pire reduit au même denominateur et utilise le fait que f(x) est de la forme u/v de derivée
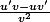
-
pandatesk
- Messages: 5
- Enregistré le: 29 Aoû 2007, 09:42
-
 par pandatesk » 29 Aoû 2007, 10:20
par pandatesk » 29 Aoû 2007, 10:20
ok j'essaye merci
-
pandatesk
- Messages: 5
- Enregistré le: 29 Aoû 2007, 09:42
-
 par pandatesk » 29 Aoû 2007, 10:26
par pandatesk » 29 Aoû 2007, 10:26
je laisse tomber j'arrete là merci quand meme
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 29 Aoû 2007, 10:35
par fonfon » 29 Aoû 2007, 10:35
re,
bon ben
}=1-2x-\frac{4}{x})
soit
}=0-2-\frac{4}{x^2})
donc
}=\frac{-2x^2+4}{x^2})
f'(x) s'annulent en

ou en

il ne te reste plus qu'à etudier le signe de f'(x) sur ]-inf,-V2[,]-V2,0[,]0,V2[ et enfin sur ]V2,+inf[ et tu auras les variations de f
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 68 invités
