Exercice Spé maths

[cricri130189]

On considère l'ensemble E des entiers relatifs x qui vérifient simultanément:

x est congru à 2 modulo 5
x est congru à 2 modulo 7
x est congru à 2 modulo 9


Démontrer que x-2 est divisible par 35
Démontrer que x-2 est divisible par 315
Donner la forme générale des éléments de E
Déterminer les éléments de E compris entre -1000 et -500?
Quelle est la différence de deux éléments constitutifs de E?
En déduire que deux éléments de E consécutifs sont premiers entre eux.

J'ai reussi les trois premieres questions mais je bloque pour la suite donc si quelqu'un peut m'expliquer ça m'avancerait beaucoup
Merci

[tize]

Bonjour,

"x est congru à 2 modulo 5" veut dire qu'il existe un entier relatif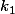 tq donc x-2 est divisible par 5.
De même "x est congru à 2 modulo 7" veut dire que x-2 est divisible par 7
x-2 est donc divisible par 5 et 7, x-2 est donc divisible par le ppcm de 5 et 7 qui est 35 (car 5 et 7 sont premiers entre eux)
"x est congru à 2 modulo 9" veut dire que x-2 est divisible par 9
De même x-2 est divisible par 35 et 9, x-2 est donc divisible par le ppcm de 35 et 9 qui est 315 (car 35 et 9 sont premiers entre eux).
Pour conclure, les nombres vérifiant :
x est congru à 2 modulo 5
x est congru à 2 modulo 7
x est congru à 2 modulo 9
sont des nombres x tels que x-2 est divisible par 315 et réciproquement si y est un nombre tel que y-2 est divisible par 315, on constate que:
y est congru à 2 modulo 5
y est congru à 2 modulo 7
y est congru à 2 modulo 9
Les nombres recherchés sont donc de la forme : avec 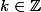(il est facile de trouver ceux compris entre -1000 et -500). La différence entre deux éléments consécutifs de E est donc 315.
Soient x et y deux nombres consécutifs de E, on a donc par exemple : x=y+315 et m un diviseur de x et y, grâce à x=y+315, on sait que si m divise x et y alors m divise 315=3*3*5*7, et m est lui même divisible par 3, 5 ou 7 (ou plusieurs d'entre eux à la fois) ou alors m=1 et puisque x et y ne sont pas divisibles par, 3,5 ou 7 on a donc m=1 ce qui veut dire que le seul diviseur de x et y est 1 autrement x et y sont premiers entre eux.