Problemes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nico33620
- Membre Naturel
- Messages: 31
- Enregistré le: 10 Jan 2007, 15:34
-
 par nico33620 » 11 Fév 2007, 15:56
par nico33620 » 11 Fév 2007, 15:56
bonjour voici le probleme
Un triangle rectangle a pour perimetre 154 cm et pour aire 924 cm²
quelle est la longueur de l'hypothenuse?
merci d'avance pour l'aide car sa fais plus d'une heure que je bloke sur cet exercice
-
nico33620
- Membre Naturel
- Messages: 31
- Enregistré le: 10 Jan 2007, 15:34
-
 par nico33620 » 11 Fév 2007, 16:13
par nico33620 » 11 Fév 2007, 16:13
personne ne peut repondre :triste:
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 11 Fév 2007, 16:17
par euclide » 11 Fév 2007, 16:17
Il faut résoudre ce système :
c est l'hypothénuse et a et b sont les deux autres côtés

-
nico33620
- Membre Naturel
- Messages: 31
- Enregistré le: 10 Jan 2007, 15:34
-
 par nico33620 » 11 Fév 2007, 16:26
par nico33620 » 11 Fév 2007, 16:26
dsl mais je bloque toujours
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 11 Fév 2007, 16:28
par euclide » 11 Fév 2007, 16:28
En fait comme tu ne veux que l'hypothénuse tu n'est pas obligé de résoudre ce système complètement mais juste d'utiliser ces équations pour trouver la valeur de c.
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 11 Fév 2007, 16:31
par euclide » 11 Fév 2007, 16:31
On a : a+b+c=154 car le périmètre est de 154 cm
ab/2=924 car l'aire vaut 924 cm²
et a²+b²=c² car le triangle est rectangle avec c comme hypothénuse
tu peux réécrire la première équation : a+b=154-c puis met cette équation au carré et utilise les autres équations...
-
nico33620
- Membre Naturel
- Messages: 31
- Enregistré le: 10 Jan 2007, 15:34
-
 par nico33620 » 11 Fév 2007, 16:38
par nico33620 » 11 Fév 2007, 16:38
ui mé justement c sur les équations que je bloke
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 11 Fév 2007, 16:39
par euclide » 11 Fév 2007, 16:39
a+b+c=154
a+b=154-c
(a+b)²=(154-c)²
a²+2ab+b²=154²-2x154xc+c²
a²+b²=23716-308c+c²-2ab
or on connait "a²+b²" en fonction de c et "ab", donc on peut obtenir une équation à une seule inconnue (qui est c) en remplaçant...
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 11 Fév 2007, 16:46
par euclide » 11 Fév 2007, 16:46
Dans la dernière équation tu peux remplacer par c² (d'après la troisième équation du système en haut) et tu peux remplacer ab par 924x2 (d'après la deuxième équation du système en haut)...puis les c² se simplifient et après résolution de l'équation tu trouves c=65.
-
nico33620
- Membre Naturel
- Messages: 31
- Enregistré le: 10 Jan 2007, 15:34
-
 par nico33620 » 11 Fév 2007, 16:49
par nico33620 » 11 Fév 2007, 16:49
dsl mé jcomprend pas :triste:
-
euclide
- Membre Relatif
- Messages: 100
- Enregistré le: 10 Aoû 2006, 13:22
-
 par euclide » 11 Fév 2007, 16:56
par euclide » 11 Fév 2007, 16:56
Récapitulons, on a :
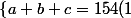\\ab/2=924(2)\\a^2+b^2=c^2(3))
On a (1) car le périmètre est de 154, (2) car l'aire est de 924, (3) car le triangle est rectangle.
A partir de (1) on trouve :
a+b+c=154
a+b=154-c
(a+b)²=(154-c)²
a²+2ab+b²=154²-2x154xc+c²
a²+2ab+b²=23716-308c+c²
Ensuite avec (3) et (2) :
en effet a²+b²=c²
c²+2x2x924=23716-308c+c² car on a ab/2=924 donc ab=2x924
3696=23716-308c
308c=20020
c=65
-
nico33620
- Membre Naturel
- Messages: 31
- Enregistré le: 10 Jan 2007, 15:34
-
 par nico33620 » 11 Fév 2007, 16:57
par nico33620 » 11 Fév 2007, 16:57
merci pour l'aide
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 182 invités
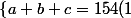\\ab/2=924(2)\\a^2+b^2=c^2(3))
