Barycentres

[capuchouchou]

Comment peut-on démontrer, en ayant un triangle ABC dont chacun des côtés est partagé en trois segments de même longueur, que les droites (IL), (JM) et (KN) concourent au centre de gravité G du triangle?

une petite image pour plus de clarté:
[img][IMG]http://membres.mezimages.com/image/capuchouchou/triangle.jpg[/img][/IMG]

[armor92]

Bonjour capuchouchou,

On peut démontrer que le centre de gravité G est le milieu commun des segments [IL], [JM] et [KN]

Pour démontrer que G est le milieu de [IL], démontrons que :
+ =

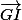I est au tiers du segment[AB] du coté de A peut s'exprimer par le fait que I est le barycentre de (A,2) et de (B,1).

On a donc le relation :
3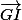 = 2 +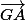

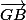
De même L est au tiers du segment[BC] du coté de C peut s'exprimer par le fait que L est le barycentre de (C,2) et de (B,1).

On a donc le relation :
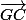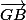
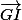3 = 2 +

+ = (2 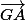+ 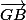) / 3 + (2 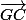+ 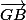) / 3 =
2 / 3 ( + + )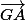

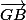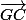On sait que G est barycentre du triangle ABC, donc on a la relation :
+ + =

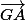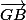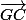Ona démontré que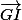 + = , donc G est le milieu du segment [IL]

La démonstration est similaire pour démontrer que G est milieu du segment [JM] et du segment [KN]

[capuchouchou]

Merci beaucoup pour cette réponse rapide! je vais essayer avec ça! :we: