Probabilités

[FlorianeSP]

Serait-il possible d'avoir de l'aide pour cet exercice, dont je ne comprend rien du tout ! Pour cela, je vais mettre le début de l'énoncé, afin que vous puissiez m'aider à avoir quelques pistes pour commencer ! Merci d'avance !

Enoncé :

On dispose de deux urnes U1 et U2 contenant des boules indiscernables au toucher.
U1 contient n boules blanches et 3 boules noires (n est un entier supérieur ou égale à 1).
U2 contient 2 boules blanches et 1 boule noire.
On tire au hazard une boule de U1 et on la met dans U2, puis on tire au hazard une boule de U2 et on la met dans U1 ; l'ensemble de ces opérations constitue une épreuve.
1. On considère l'évènement A >.
a. Montrer que la probabilité p(A) de l'évènement A peut s'écrire :
p(A)=3/4(n+2/n+3).
2. On considère l'évènement B >.
Vérifier que la probabilité p(B) de l'évènement B peut s'écrire :
p(B)=6/(4(n+3)).

[BancH]

Pour que l'événement ait lieu, il faut soit tirer une boule noire dans les deux urnes soit une blanche.

La probabilité de tirer une boule noire dans est
La probabilité de tirer une noire dans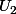 si une noire a été tirée dans est
Une blanche dans :
Blanc dans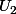 si blanc dans :

Ainsi

C'est bien le résultat voulu.

[BancH]

Pour que l'événement se réalise, il faut que la boule tirée dans soit noire () car si elle est blanche, alors il y aura trois boules blanches dans et après le second tirage, il restera au minimum deux boules blanches.
Il faut aussi que lors du second tirage, la boule tirée soit blanche ().

[FlorianeSP]

Merci beaucoup pour ce coup de main !
Cordialement.
FlorianeSP

[BancH]

Ok ......