Bonjour à tous et bonne année
Voila j'ai un petit souci sur l'intégrale suivante:
Intégrale de 0 à 2pi de : ln(1-2.alpha.cos(x)+alpha^2)dx
alpha appartenant a R*+
Je ne fais pas comment partir !
un cdv si oui lequel?
ou un encadrement par les sommes de Rieman?
Merci pour votre aide
Intégrale
14 messages
- Page 1 sur 1
mathelot a écrit:bonjour Tize,
pourrais tu poster le résultat de Mathematica ? je suis vraiment curieux de
voir quelle tête il a.
Pas de problème; mais tu pourra le constater par toi même en ecrivant : Log[1-2*a*Cos[x]+a^2] sur cette page., le résultat étant vraiment trop vilain pour être écrit...
Pour être honnéte, j'avais posé la question sur 2 forums différents et un de vos collégues matheux à trouver une solution intéressante mais plutôt difficile à comprendre (du moins pour moi 
Le raisonnement est expliqué sur le lien suivant:
http://www.maths-express.com/forum/detail.php?forumid=4&id=27225&p=1
merci
Le raisonnement est expliqué sur le lien suivant:
http://www.maths-express.com/forum/detail.php?forumid=4&id=27225&p=1
merci
De quelle intégrale veut-tu parler? L'intégrale de départ?
Merci de jetter un oeil sur le raisonnement du matheux sur le lien précédent:
http://www.maths-express.com/forum/detail.php?forumid=4&id=27225&p=1
Merci de jetter un oeil sur le raisonnement du matheux sur le lien précédent:
http://www.maths-express.com/forum/detail.php?forumid=4&id=27225&p=1
D'après Methodix Analyse chapître 19 page 279
on regarde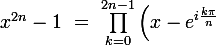 \ = \ \prod_{k=0}^{n-1} \left ( x - e^{i\frac {k\pi}{n}} \right ) \left ( x - e^{-i\frac {k\pi}{n}} \right )(x-1)(x+1))
(en regroupant les termes conjugués à k et n-k)
Cette relation donne facilement celle suggérée par l'énoncé et conduit à :
 + 1 \right ) = \frac {(x^{2n} - 1)(x^2 - 2x + 1)}{x^2 - 1} \ = \ \frac {(x^{2n} - 1)(x+1)}{x-1})
On passe au logarithme népérien et donc en effet on utilise les sommes de Riemann :
 + 1)dt = \lim_{n \rightarrow \infty} \frac {\pi}{n} \sum_{k=1}^n ln\left ( r^2 - 2.r.cos \frac {k\pi}{n} + 1 \right ) = \lim_{n \rightarrow \infty} \frac {\pi}{n} ln \frac{(r^{2n}-1)(r+1)}{r-1})
Il faut alors distinguer selon |r| :
- si |r| > 1 : I = 2 ln |r|
ln |r|
- si |r| < 1 : I = 0
Donc voilà je t'ai recopier le corrigé de l'exo sans rien comprendre lol
Enfin si le départ , les racines n-iéme de x^2n - 1 qui sont complexes et conjuguées tout ça tout ça quoi
, les racines n-iéme de x^2n - 1 qui sont complexes et conjuguées tout ça tout ça quoi
Voilà bon courage
on regarde
(en regroupant les termes conjugués à k et n-k)
Cette relation donne facilement celle suggérée par l'énoncé et conduit à :
On passe au logarithme népérien et donc en effet on utilise les sommes de Riemann :
Il faut alors distinguer selon |r| :
- si |r| > 1 : I = 2
- si |r| < 1 : I = 0
Donc voilà je t'ai recopier le corrigé de l'exo sans rien comprendre lol
Enfin si le départ
Voilà bon courage
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
