Exercice sur les aplications linéaires

[ayla8101]

On note f l'application qui a tout polynome P (de degré inférieur ou égal à 2) de E (espace vectoriel des polyniomes de degré inférieur ou égal à2) associe la fonction Q=P(x)+(2x-1)P'(x)+1/2(x²-x)P"(x).

J'ai déterminé que pour les valeurs 1,3 et 6, l'application g(a)=f-aId n'est pas bijective (Id : application identité) ( en utilisant le fait que (1,x,x²) est une base de E et enécrivant la matrice de f dans cette base B).

Je dois à présent déterminer pour chacune de ces valeurs (cad 1,3 et 6) le noyau, le rang et l'image de g(a).
Sauf que je bloque complètement!
Pourriez vous m'aider, SVP?

[ayla8101]

Personne n'a une piste?

[mathelot]

Par exemple, pour la valeur propre :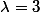
on pose .
on suppose que
on regarde le nombre de degré de liberté du système obtenu et ça donne
une base de ker(g).
pour le rang:
rang((g(3)))=dim(E)-dim(ker(g(3))=3-dim(ker(g(3))
Dans cette question est quelconque.
pour une base de Im(g(3)), on écrit le vecteur comme combinaison linéaire de vecteurs indépendants.

[ayla8101]

Oula, ce que tu fais est beaucoup plu compliqué que ce que je fais d'habitude! Concentrons nous sur le noyau : pourrais tu un peu plus détailler? On me demande de trouver le noyau etnon pas une base. Et que veut dire " on regarde le nb de degré de liberté du système obtenu"?

[mathelot]

Et que veut dire " on regarde le nb de degré de liberté du système obtenu"?

c'est le nombre d'inconnues que tu prends comme paramètres.
exemple:
2x-y=0
cad:
y=2x
1 degré de liberté: x
puis:
x=x
y=2x
ton vecteur est proportionnel à .