Domaine de définition développement limité

[Clemaac]

Bonjour,

Dans mon cours, il est dit que pour calculer le développement en 0 d'une fonction f, il faut que f soit défini au voisinage de 0.De ce que j'en ai compris, le domaine de définition de f est un intervalle ouvert autour de 0, donc contenant 0.

De plus, si f admet un développement limité en 0, alors f est au moins de classe C^1.

Pourtant on peut calculer le développement limité de f(x)= x/ln(1+x) à n'importe quelle ordre alors que f n'est ni définie ni dérivable en 0.

Faut-il prolonger d'abord la fonction par continuité en 0? Pourtant dans mon exercice le prolongement vient après le calcul du DL de x/ln(x).

Merci de vos réponses, j'ai peut être quelques lacunes vis à vis de la continuité/ dérivabilité donc je ne comprends pas bien.

[Ben314]

Salut,
Tu as qu'à dire que le fait que " soit définie au voisinage de ", ça signifie que est définie au moins sur un intervalle ouvert "épointé", c'est à dire privé de .
Et en fait, on peut même donner du sens à un développement limité dés que la fonction est définie pour une suite de points qui tendent vers de façon à pouvoir calculer des limites de lorsque tend vers .
Par exemple une fonction qui ne serait définie que pour les , on pourrait (essayer de) calculer le D.L. en 0 de la fonction.
Par contre, si la fonction n'était définie que sur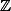 , ça n'aurait pas de sens de chercher un D.L. en 0 vu qu'on a pas de points qui peuvent tendre vers 0 (à part en étant constamment égal à 0 bien sûr)

[Clemaac]

D'accord merci beaucoup!

Donc si j'ai bien compris le fait que la fonction soit définie en 0 ou dérivable en 0 est principalement importante pour avoir un DL avec l'aide de la formule de Taylor Young. Mais une fonction définie sur un intervalle autour de 0, sauf en 0 par exemple peut avoir unDL en 0. Il faudra par contre le trouver à l'aide d'une composition de DL ou autre.

[Ben314]

Oui, c'est ça.