Domaine de définition de ln(x^3-y^3)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 07 Fév 2010, 09:11
par MacErmite » 07 Fév 2010, 09:11
Bonjour,
Pouvez-vous m'aider à trouver le domaine de définition de cette fonction :
 = ln (x^3-y^3))
j'ai écris que

d'ou
(x^2+y^2-yx) >0)
ce qui conduit à x>y. Ensuite cela dépend du signe de

soit [TEX] yx y et yx < 0
Mais est-ce juste ? je n'arrive pas à me représenter la future surface engendrée par f(x,y) avec les conditions sur x et y ...
Merci.

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 07 Fév 2010, 09:25
par fatal_error » 07 Fév 2010, 09:25
salut,
on peut remarquer que
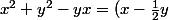^2 + \frac{3}{4}y^2)
C'est strictement positif si x et y sont différents de 0
la vie est une fête

-
MacErmite
- Membre Relatif
- Messages: 408
- Enregistré le: 12 Mai 2006, 12:00
-
 par MacErmite » 07 Fév 2010, 09:36
par MacErmite » 07 Fév 2010, 09:36
fatal_error a écrit:salut,
on peut remarquer que
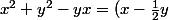^2 + \frac{3}{4}y^2)
C'est strictement positif si x et y sont différents de 0
Donc la condition xy 0[/TEX] , de plus

pour tout x et y j'en avais conclu la deuxième condition : xy<0. Ce qui apparement est faux, mais je ne comprends pas pourquoi ?
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 07 Fév 2010, 10:05
par Sylviel » 07 Fév 2010, 10:05
C'est une histoire de conditions suffisante ou nécessaire. Si xy<0 ça marche, c'est sûr, mais ce n'est pas nécessaire : en effet tu as remplacé x²+y² par 0, alors que parfois x²+y² est bien plus grand que 0... D'ailleurs il existe une inégalité souvent bien pratique (et à connaître): xy <= (x²+y²)/2 (a toi de le démontrer)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Fév 2010, 10:09
par Ben314 » 07 Fév 2010, 10:09
Salut,
C'est un problème de logique. Considère les quantitées suivantes :
A=x²+y² ; B=-xy ; C=A+B=x²+y²-xy
Comme A>0, on a effectivement (B>0 => A+B>0)
Mais la réciproque est fausse : A+B>0 n'implique pas B>0,
par exemple 8+(-3)>0 alors que -3 n'est pas positif.
Pour ton problème de départ, tu peut aussi directement écrire :
x^3-y^3>0 <=> x^3>y^3 <=> x>y
Car la fonction t->t^3 est strictement croissante sur R.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités