Preuve d'un simple exercice

[Guillermo]

Bonjour à tous,
Je dois prouver ce théorème : "If x and y are arbitrary real numbers with x < y, prove that there is at least one real z satisfying x < z < y."
Voici la (courte) preuve du théorème selon mon livre :
"0 < y − x.
⇒ n(y − x) > h > 0, n ∈ Z+, h arbitrary
y − x > h/n ⇒ y > x + h/n > x
so let z = x + h/n Done."
La seule chose que je ne comprends pas, c'est le passage en gras : on considère un nombre arbitraire h réel positif, mais qu'est-ce qui nous permet de dire qu'il est à la fois supérieure à 0 et inférieur à n(y - x) ? C'est la seule chose que je ne comprends pas dans cette preuve.

[Ben314]

C'est de plus en plus n'importe quoi ton bouquin . . .

Pour montrer qu'il existe un réel strictement entre et (avec 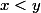fixés), ça me semblerais quand même un soupçon plus simple (et plus constructif...) de bêtement considérer .
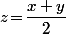(Et c'est aussi bien plus malin de procéder comme ça du fait que le résultat reste vrai dans tout corps totalement ordonné, qu'il soit Archimédien ou pas)

Et sinon, dans le bouquin, on te dit que est "arbitraire" (strictement positif) donc tu prend ce que tu veut et la preuve me semblerais moins alambiquée si elle prenait simplement 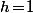épicétout (là, ça donne on ne peut plus l'impression d'être du "pourquoi faire simple quand on peut faire compliqué . . .)

Et pour répondre précisément à tes questions :
- Pourquoi le est strictement positif ? => Parce qu'on l'a choisi comme ça.
- Pourquoi est-il strictement plus petit que => Parce qu'il y a un des axiomes de R (appelé axiome d'Archimède) qui dit que, étant donné deux réels strictement positifs (ici et ), il existe au moins un entier naturel tel que fois le premier nombre soit plus grand que le deuxième. Donc, dans la prose (merdique) du bouquin, à mon avis, ce qu'il faut comprendre, c'est que l'on commence par choisi un réel (n'importe lequel, donc par exemple 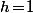) puis on utilise l'axiome d'Archimède pour dire qu'il existe un entier naturel tel que

[Guillermo]

Merci, mais je ne vois pas quelle démarche on pourrait faire pour arriver à x < (x+y)/2 < y, après avoir supposé que z = (x+y)/2...

[Ben314]

x < (x+y)/2 < y équivaut (en multipliant par 2) à 2x < x+y <2y
2x < x+y équivaut (en retranchant x) à x < y (vrai par hypothèse)
x+y < 2y équivaut (en retranchant y) à x < y (vrai par hypothèse)