Borne inférieure de S

[Guillermo]

Bonjour, je ne comprends pas la preuve de ce théorème :

Theorem : Every nonempty set S that is bounded below has a greatest lower bound ; that is, there is a real number L such that L = inf S (c'est-à-dire infimum of S)
Proof : Let -S denote the set of negatives of numbers in S. Then -S is nonempty and bounded above. Axiom 10 tells us that there is a number B which is a supremum for -S. It is easy to verify that -B = inf S.
Axiome 10 : Every nonempty set S of real numbers which is bounded above has a supremum; that is, there is a real number B such that B = sup S.

Je ne comprends pas les deux passages en gras : pourquoi le fait que -S soit l'ensemble des opposés de tous les nombres de S implique que -S est non-vide et que -S possède une borne supérieure ?
Et ce qui m'énerve dans les manuels de maths c'est que souvent l'auteur passe des étapes lors de l'explication des preuves et des démonstrations, c'est le cas lorsqu'il écrit "It is easy to verify that -B = inf S" : je ne sais pas vraiment comment il arrive à une telle phrase...
Merci de votre aide !

[GaBuZoMeu]

Bonjour,

Deux choses :
1) Si est non vide (contient au moins un élément ), alors 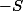est non vide. je suis sûr que tu peux en donner un élément.
2) Si a un minorant (c'est ce que veut dire "bounded below"), c.-à-d. si est inférieur ou égal à tout élément de , alors 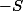a un majorant (qui est supérieur ou égal à tout élément de 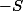) ; c'est ça "bounded above". Je suis sûr que tu peux donner un tel majorant.

[Guillermo]

OK ! Mes réponses :
1) un élément de -S : -x
2) un majorant de -S : -m
Et concernant la phrase "It is easy to verify that -B = inf S", trouves-tu ça suffisant comme "preuve mathématique" ?... Dire que "it is easy to verify...", ça me semble pas très rigoureux pour clôturer une preuve mathématique...

[Ben314]

Salut,
Perso., ça me choque pas plus que de raison : normalement il est acquis dès début du collège (au moment où on défini les nombres négatifs en fait) que, lorsque l'on prend les opposés de deux réels, ça inverse l'ordre dans lequel ils sont : .
Et ça implique immédiatement que :

puis que