Salut à tous !
Bon ça a beau être les vacances, faut quand même travailler, alors j'espère que sur ce point vous pourrez m'aider!
Vala les énoncés :
Exercice I
1°) Etude d'un exemple
Dans un cube ABCDEFGH, soit I le centre de la face ABFE et J, K et L les milieux respectifs des arrêtes [AB], [EH] et [AD].
a - Démontrer que le triangle CIK est rectangle en I
b - Justifier que les points J et L sont les projetés orthogonaux respectifs des points I et K sur le plan (ABC)
c - Le triangle CJL est-il rectangle en J ? justifier
2°) Soit un triangle OMN rectangle en O, et un plan P qui n'est orthogonal à aucun des côtés du triangle OMN. on note respectivement O' , M' , et N' les projetés orthogonaux des points O, M et N sur le plan P
a - On suppose que la droite (OM) est parallèle au plan P. Démontrer que le triangle O'M'N' est rectangle en O'.
b - On suppose que la droite (OM) n'est pas parallèle au plan P et que le triangle O'M'N' est rectangle en O'. Démontrer que la droite (ON) est orthogonale au plan (OMM'). En déduire que la droite (ON) est parallèle au plan P.
c - Enoncer le théorème démontré dans les questions a - et b -
3°) Application
Soit SABCD une pyramide à base carrée ABCD telle que (AS) est orthogonale au plan (ABC). Soit E et F les milieux es arrêtes [SA] et [SB] et G un poiint de l'arrête [SC] distinct du milieu de [SC].
Démontrer que la section de la pyramide SABCD par le plan (EFG) est un trapèze rectangle.
Exercice II
Soit ABCD un tétraèdre régulier et M est un point libre du segment [BC] distinct de B et de C.
1°) Démontrer que la section du tétraèdre ABCD par le plan P passant par M et orthogonale à la droite (BC) est un triangle isocèle MNP.
2°) On note I, J, Q les milieux respectifs des segments [BC], [AD], [NP]
a - Démontrer que si M appartient au segment [CI], alors Q appartient au segment [CJ].
b - Déterminer le lieu géométrique du point Q lorsque M décrit le segment [CI] privé du point C.
3°) Etudier le lieu géométrique du centre de gravité G du triangle MNP lorsque M décrit le segment [BC] privé de B et de C.
Je suis vraiment bloquée, je comprends même pas l'énoncé.
J'espère que vous pourrez vite m'aider.
Merci !
Géométrie dans l'espace
12 messages
- Page 1 sur 1
Pour démontrer que le triangle CIK est rectangle en I, il faut se placer dans le plan BCHE, c'est à dire le plan qui coupe le cube par sa diagonale.
BCHE est un rectangle (attention pas un carré ! ), dont le coté BC = c (coté du cube) et BE = Racine (2) * c (diagonale de la face supérieure du cube)
I est le milieu du coté BE, K est le milieu du coté EH.
Il faut démontrer que IC² + IK² = CK².
On peut écrire (théorème de pythagore):
CK² = KH² + HC² = c²/4 + 2c²
KI² = EK² + EI² = c²/4 + c²/2
IC² = IB² + BC² = c²/2 + c²
Il suffit de vérifier qu'on a bien la relation cherchée.
BCHE est un rectangle (attention pas un carré ! ), dont le coté BC = c (coté du cube) et BE = Racine (2) * c (diagonale de la face supérieure du cube)
I est le milieu du coté BE, K est le milieu du coté EH.
Il faut démontrer que IC² + IK² = CK².
On peut écrire (théorème de pythagore):
CK² = KH² + HC² = c²/4 + 2c²
KI² = EK² + EI² = c²/4 + c²/2
IC² = IB² + BC² = c²/2 + c²
Il suffit de vérifier qu'on a bien la relation cherchée.
Bonjour
Une piste à explorer est la géométrie analytique
Soit le repère (A,AB,AD,AE) "je ne mets pas le symbole des vecteurs"
Ecrire les coordonnées des points A, B, C, D, E, F, G, H, I, J, et K
A(0,0,0) B(1,0,0)..........et K(0, ,1)
,1)
Ecrire les coordonnées des vecteurs IC, IK, et KC
IC( ,1,-
,1,- ) ...........
) ...........
Pour terminer, on montre que +
+ =
=  =
= 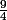
La suite t'appartient ..............
Cordialement
Une piste à explorer est la géométrie analytique
Soit le repère (A,AB,AD,AE) "je ne mets pas le symbole des vecteurs"
Ecrire les coordonnées des points A, B, C, D, E, F, G, H, I, J, et K
A(0,0,0) B(1,0,0)..........et K(0,
Ecrire les coordonnées des vecteurs IC, IK, et KC
IC(
Pour terminer, on montre que
La suite t'appartient ..............
Cordialement
personnellement, j'ai fait ceci, je ne sais pas si c'est une bonne méthode alors dites moi si j'ai fait des erreurs
On appelle a la longueur de l'arête du cube. On calcule les longueurs de chacun des côtés du triangle ICK.
Rappels : 1) la diagonale d'un carré de côté a a pour longueur a racine de 2.
2) Dans un triangle équilatéral de côté c , une médiane a pour mesure (coté x racine de 3)/2:
Le triangle ACF est équilatéral de côté , I est le milieu de [AF] donc [CF] est une médiane de ce triangle, par conséquent CF = (a racine de 2)x(racine de 3 /2) = (a racine de 6)/2
La droite (KE) est orthogonale au plan (ABFE) donc à la droite (EB). Le triangle KEI est donc rectangle en E.
KI²=KE² + EI²= (a/2)² + (a racine de 2 /2)²= (3a²)/4
La droite (KH) est orthogonale au plan (HGCD) donc à la droite (HC). Le triangle KHC est rectangle en H.
KC² = KH² + HC²= (a/2)² + (a racine de 2)²= (9a²)/4
Il reste à montrer que le théorème de Pythagore est vérifié.
KI² + IC²= (3a²)/4 + (a racine de 6 / 2)²=(9a²)/4=KC²Le triangle ICK est donc rectangle en I
Pour la suite, j'aurai une question : existe-t-il une méthode particulière pour démontrer que des points sur un certain plan sont les projetés orthogonaux d'autres points ?
Faut-il utiliser des mesures de longueur ou expliquer que (IJ) étant orthogonal au plan (ABC) et J appartenant à (IJ) et au plan (ABC), J est le projeté orthogonal de I sur (ABC)?
Si c'est cela qu'il faut faire, pour démontrer que L est le projeté orthognal de K sur (ABC), peut-on dire que, comme (KL) est orthogonal à (ABC) et que L appartient à (ABC); alors L est le projeté orthogonal de K sur (ABC) ?
On appelle a la longueur de l'arête du cube. On calcule les longueurs de chacun des côtés du triangle ICK.
Rappels : 1) la diagonale d'un carré de côté a a pour longueur a racine de 2.
2) Dans un triangle équilatéral de côté c , une médiane a pour mesure (coté x racine de 3)/2:
Le triangle ACF est équilatéral de côté , I est le milieu de [AF] donc [CF] est une médiane de ce triangle, par conséquent CF = (a racine de 2)x(racine de 3 /2) = (a racine de 6)/2
La droite (KE) est orthogonale au plan (ABFE) donc à la droite (EB). Le triangle KEI est donc rectangle en E.
KI²=KE² + EI²= (a/2)² + (a racine de 2 /2)²= (3a²)/4
La droite (KH) est orthogonale au plan (HGCD) donc à la droite (HC). Le triangle KHC est rectangle en H.
KC² = KH² + HC²= (a/2)² + (a racine de 2)²= (9a²)/4
Il reste à montrer que le théorème de Pythagore est vérifié.
KI² + IC²= (3a²)/4 + (a racine de 6 / 2)²=(9a²)/4=KC²Le triangle ICK est donc rectangle en I
Pour la suite, j'aurai une question : existe-t-il une méthode particulière pour démontrer que des points sur un certain plan sont les projetés orthogonaux d'autres points ?
Faut-il utiliser des mesures de longueur ou expliquer que (IJ) étant orthogonal au plan (ABC) et J appartenant à (IJ) et au plan (ABC), J est le projeté orthogonal de I sur (ABC)?
Si c'est cela qu'il faut faire, pour démontrer que L est le projeté orthognal de K sur (ABC), peut-on dire que, comme (KL) est orthogonal à (ABC) et que L appartient à (ABC); alors L est le projeté orthogonal de K sur (ABC) ?
C'est bon en fait j'ai réussi
Il ne reste plus que le 2°) et le 3°)
Il ne reste plus que le 2°) et le 3°)
Simply a écrit:
2°) Soit un triangle OMN rectangle en O, et un plan P qui n'est orthogonal à aucun des côtés du triangle OMN. on note respectivement O' , M' , et N' les projetés orthogonaux des points O, M et N sur le plan P
a - On suppose que la droite (OM) est parallèle au plan P. Démontrer que le triangle O'M'N' est rectangle en O'.
b - On suppose que la droite (OM) n'est pas parallèle au plan P et que le triangle O'M'N' est rectangle en O'. Démontrer que la droite (ON) est orthogonale au plan (OMM'). En déduire que la droite (ON) est parallèle au plan P.
c - Enoncer le théorème démontré dans les questions a - et b -
3°) Application
Soit SABCD une pyramide à base carrée ABCD telle que (AS) est orthogonale au plan (ABC). Soit E et F les milieux es arrêtes [SA] et [SB] et G un poiint de l'arrête [SC] distinct du milieu de [SC].
Démontrer que la section de la pyramide SABCD par le plan (EFG) est un trapèze rectangle.
2°) On note I, J, Q les milieux respectifs des segments [BC], [AD], [NP]
a - Démontrer que si M appartient au segment [CI], alors Q appartient au segment [CJ].
b - Déterminer le lieu géométrique du point Q lorsque M décrit le segment [CI] privé du point C.
3°) Etudier le lieu géométrique du centre de gravité G du triangle MNP lorsque M décrit le segment [BC] privé de B et de C.
J'ai réussi la a), mais pas le reste
s'il vous plait, c'est urgent !
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

