Bonjour tout le monde,
Pour un devoir de probabilité, un de nos exercices nous demande de considérer, sur un segment ordonné de 0 à A, un processus : une particule par d'un point B, elle a, en fonction de sa position k/A chances d'aller à droite, et le conjugué à gauche (exemple, à B ma particule à B/A chances d'aller à B+1 et 1 -B/A d'aller à B-1). Le processus se termine quand la particule à atteint 0 ou A, quelle est alors la probabilité qu'il finisse en A ?
Pour répondre à cette question, j'ai essayé de faire une suite par récurrence d'ordre 2 tel que, U(n) = [n/A]U(n+1) + [1-n/A]U(n-1). Ne sachant pas comment résoudre une suite par récurrence linéaire d'ordre 2 à coefficients non constants, je me tourne en dernier espoir vers vous.
Merci d'avance pour votre réponse.
Terme général d'une suite récurrente
3 messages
- Page 1 sur 1
Re: Terme général d'une suite récurrente
Indice : Chaines de Markov.
Tu as une matrice de transition. Matrice carrée avec A+1 lignes et A+1 colonnes. Il y a des 0 partout, sauf sur les 2 ""diagonales"" de part et d'autre de la diagonale descendante. Sur chaque ligne, la somme des 2 termes vaut 1. Cette matrice, tu peux l'élever à la puissance n, et calculer sa limite quand n tend vers l'infini.
Elevée à l'infini, cette matrice a des 0 partout, sauf en 1ère et dernière colonnes.
Et ensuite, tu multiplies cette matrice par le vecteur ayant des 0 partout, sauf un 1 en ligne B+1. Autrement dit, tu regardes la ligne B+1 de cette matrice.
Tu as une matrice de transition. Matrice carrée avec A+1 lignes et A+1 colonnes. Il y a des 0 partout, sauf sur les 2 ""diagonales"" de part et d'autre de la diagonale descendante. Sur chaque ligne, la somme des 2 termes vaut 1. Cette matrice, tu peux l'élever à la puissance n, et calculer sa limite quand n tend vers l'infini.
Elevée à l'infini, cette matrice a des 0 partout, sauf en 1ère et dernière colonnes.
Et ensuite, tu multiplies cette matrice par le vecteur ayant des 0 partout, sauf un 1 en ligne B+1. Autrement dit, tu regardes la ligne B+1 de cette matrice.
Re: Terme général d'une suite récurrente
Bonjour,
C'est vrai qu'il y a une chaîne de Markov absorbante derrière ça, mais je crains que ça ne t'avance pas beaucoup.
Reprenons ce que tu avais commencé. Ton) est visiblement la probabilité de terminer en
est visiblement la probabilité de terminer en  en partant de
en partant de  . On a effectivement
. On a effectivement =0) ,
, =1) et
et  = \dfrac{n}{A}U(n+1) + \dfrac{A-n}{A}U(n-1)) pour
pour  . Ce n'est donc pas une suite infinie ! On a en fait un nombre fini d'inconnues et un système fini d'équations.
. Ce n'est donc pas une suite infinie ! On a en fait un nombre fini d'inconnues et un système fini d'équations.
Une astuce : il peut être avantageux de poser=U(n+1)-U(n)) pour
pour 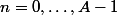 . Peux-tu écrire la relation de récurrence qui donne
. Peux-tu écrire la relation de récurrence qui donne ) en fonction de
en fonction de ) ? Écrire alors
? Écrire alors ) en fonction de
en fonction de  et de
et de ) ? Et en se souvenant que
? Et en se souvenant que 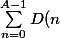= U(A)-U(0)=1) , déterminer
, déterminer ) et
et ) ?
?
C'est vrai qu'il y a une chaîne de Markov absorbante derrière ça, mais je crains que ça ne t'avance pas beaucoup.
Reprenons ce que tu avais commencé. Ton
Une astuce : il peut être avantageux de poser
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
