Théorème de Cantor-Bernstein

[samprepa]

Bonjour, j'ai ici dans l'entracte de mon devoir l'énoncé du théorème de Cantor Bernstein qui me dit que si on a une injection de E dans F et une injection de F dans E alors il existe une bijection de E sur F.
Je bloque à une question où l'on demande de justifier qu'il existe une bijection de E sur F sachant qu'il existe une injection et une surjection de E sur F.
En réalité on a juste à montrer que l'existence de cette injection de cette surjection implique l'existence d'une injection de F sur E mais je n'y suis pas parvenu. J'ai essayé de partir de la définition d'une surjection puis d'une injection et de travailler avec les fonctions composés mais ça n'a pas aboutit.
Merci pour votre aide.

[GaBuZoMeu]

Bonjour,
L'existence d'une injection de dans quand on a une surjection de sur est une conséquence de l'axiome du choix : pour chaque 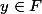, on choisit (qui est non vide par hypothèse) et on pose .