Isométrie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Kruslen
- Membre Naturel
- Messages: 13
- Enregistré le: 27 Déc 2021, 23:23
-
 par Kruslen » 11 Avr 2022, 21:54
par Kruslen » 11 Avr 2022, 21:54
Bonjour,
Je souhaiterais poser une question concernant les isométries...
Si on considère un espace préhilbertien H,
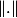
sa norme associée et

une application vérifiant f(0)=0 et :
 \in \left( \mathbb{R} \right)^{2} \, , \, \| f(x)-f(y) \| = |x-y|)
Ma question est la suivante : est-ce que la fonction définie par
=xf(1))
est la seule solution ?
J'ai l'impression que oui, mais je ne arrive pas à le prouver... J'ai seulement le fait que
 \| = |x|)
pour tout réel x, mais c'est tout

Merci pour votre aide,
Kruslen

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 12 Avr 2022, 13:15
par Ben314 » 12 Avr 2022, 13:15
Salut,
Si on prend par exemple x>1, le fait que
||f(1)-f(0)||+||f(x)-f(1)||=1+(x-1)=x=||f(x)-f(0)||
prouve que le point f(1) est situe sur le segment [f(0),f(x)] (propriete classique des prehilbetiens)
Donc f(x)=lambda.f(1) avec lambda>1 et, vu que ||f(x)||=x, c'est que lambda=x.
Meme raisonnement si 0<x<1 et si x<0.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités

