Exponentielle

[amar21]

on f(x)= (e^x+ e^-x)/2 etudier son sens de variation f et sa limite en +infini
on definit la fonction h sur (o , + oo) par h(x) =f(x)-x
resoudre l'equation e^x-eç_x-2=0
montrer que h admet un minimum m strictement positif
en donner une valeur approchée a 10^-2

[fonfon]

Bonjour déjà, qu'est-ce que tu as fait?

[amar21]

Bonjour déjà, qu'est-ce que tu as fait?

jai tout fé mais jen faisant la derivée de h jarive pa a la faire é pour l'equation je suis pa sur de ce que jai trouvé

[fonfon]

je sais pas si ce que tu as fais avant est bon mais si tu es sûr

on definit la fonction h sur (o , + oo) par h(x) =f(x)-x
resoudre l'equation e^x-eç_x-2=0

par contre je ne comprend pas ton equation

[amar21]

je sais pas si ce que tu as fais avant est bon mais si tu es sûr



par contre je ne comprend pas ton equation

desolé jai mal ecris c'est e^x - e^-x-2=0

[fonfon]

Rappel:



donc






or e^x>0 sur R donc





tu fais un petit changement de variable ....

[amar21]

Rappel:



donc






or e^x>0 sur R donc





tu fais un petit changement de variable ....

oui c'est ce que jai trouvé maintenat on me dit qu'il faut determiner h(x) comme f(x)-x on me dit de resoudre l'equation c'est ce que jai fais apres on me dit montrer que h amet un minimum m strictement positif le determiner a 10^-2

[fonfon]

as-tu derivé h(x)? tu devrais trouver un lien avec l'equation que tu viens de resoudre

[amar21]

as-tu derivé h(x)? tu devrais trouver un lien avec l'equation que tu viens de resoudre

oui mais jarrive pas a deriver h(x) c'est ca mon probleme ya un prof qui m'a dit que x apres avoir determiné l'equation equivaut a ln(1+racine carrée de 2) mais je veux pa partir sur ca jai un peu peur de me perdre comment tu la deriverai toi pour demontrer qu'il ya un minimum m positif?

[amar21]

oui mais jarrive pas a deriver h(x) c'est ca mon probleme ya un prof qui m'a dit que x apres avoir determiné l'equation equivaut a ln(1+racine carrée de 2) mais je veux pa partir sur ca jai un peu peur de me perdre comment tu la deriverai toi pour demontrer qu'il ya un minimum m positif?

on m'a dis ceci parce que cet exo fait partie du chapitre fonction logarithme

[fonfon]

moi, je deriverais h(x)
Rappel:si la fonction h a un extremum pour x, alors h'(x)=0







or d'apres le rappel il faut resoudre h'(x)=0 pour trouver le(s) extremum(a)

donc h'(x)=0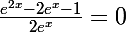 (comme 2e^x>0 sur R)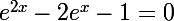

tu viens de resoudre

pour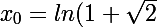 ,h'(x) passe du signe - au signe +, h est decroissabte avant x0 puis croissante apres x0, f passe par un minimum local m pour 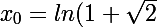dont la valeur vaut tu calcules et tu donnes 2 chiffres apres la virgule

voilà ça devrait être ça
A+

[amar21]

[quote="fonfon"]moi, je deriverais h(x)
Rappel:si la fonction h a un extremum pour x, alors h'(x)=0







or d'apres le rappel il faut resoudre h'(x)=0 pour trouver le(s) extremum(a)

donc h'(x)=0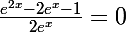 (comme 2e^x>0 sur R)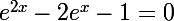

tu viens de resoudre

pour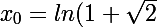 ,h'(x) passe du signe - au signe +, h est decroissabte avant x0 puis croissante apres x0, f passe par un minimum local m pour 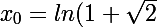dont la valeur vaut tu calcules et tu donnes 2 chiffres apres la virgule

voilà ça devrait être ça
A+[/



on me demande pour la suite on definit U0=1 et pour tout entier naturel n:
Un+1= f(un)
montrer qu'elle peut etre minorée par m pour tout entier naturel ca je lai fais en demontrant que un+1-Un equivaut a h(un) mais on me demande d'en deduire pour tout entier naturel n, Un superieur ou egal a U0+n*m puis la limite de la suite (Un)

[fonfon]

là j'ai plus trop le temps mais je te donne l'idée il faut faire une recurrence pout la limite tu sais que un>=Uo+n*m donc lim un >=lim uo+n*m qd n->+inf

[amar21]

là j'ai plus trop le temps mais je te donne l'idée il faut faire une recurrence pout la limite tu sais que un>=Uo+n*m donc lim un >=lim uo+n*m qd n->+inf

ok jai compris jei montré que u0-u1sup ou egal a m idem pour u2-U1 et tout ok jai compris mais j'ai une autre probleme on me dit discuter graphiquement f(x) = a et résoudre lorsque c'est possible cette equation ??