équation second degré 1°es
7 messages
- Page 1 sur 1
équation second degré 1°es
par vince69 » 17 Déc 2006, 09:01
""""""""""""""""""""""""""""""""""""""""""""""""""""""
par pouik » 17 Déc 2006, 09:32
Bonjour,
- a priori il faut dire que
et 
ont un point commun si il existe b tel que l'on ait :
(*)
Cherchons alors b tel que l'on ait (*) :
Cette éuqtion se réécrit sous la forme :
x+2=0)
(E)
On obtient alors un trinôme du second degré que normalement tu dois savoir résoudre (mais bon comme j'ai pas fais Es je suis pas sûr).
Calculon le discriminant
de (E) :
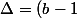^2 - 4.2.2)
- Ensuite arrivé à ce stade là tu vas pouvoir répondre en même temps à tes deux questions puisque ton Cours te dis que (E) a une unique solution (c'est-à-dire C et d ont un seul point commun) lorsque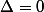
et aucun lorsque 
:
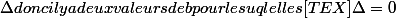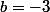et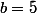 
donc deux valeurs pour que C et d aient exactement un point commun.
## 2ème cas :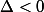
:
D'après (1) pour que soit strictement négatif il faut que :
(si tu n'es pas convaincu fais un tableau de signe).
Voilà voilà normalement j'ai assez détaillé !!! :zen: :zen: :zen: :zen: :zen:
Bonne journée.
- a priori il faut dire que
Cherchons alors b tel que l'on ait (*) :
Cette éuqtion se réécrit sous la forme :
On obtient alors un trinôme du second degré que normalement tu dois savoir résoudre (mais bon comme j'ai pas fais Es je suis pas sûr).
Calculon le discriminant
- Ensuite arrivé à ce stade là tu vas pouvoir répondre en même temps à tes deux questions puisque ton Cours te dis que (E) a une unique solution (c'est-à-dire C et d ont un seul point commun) lorsque
donc deux valeurs pour que C et d aient exactement un point commun.
## 2ème cas :
D'après (1) pour que
Voilà voilà normalement j'ai assez détaillé !!! :zen: :zen: :zen: :zen: :zen:
Bonne journée.
par pouik » 17 Déc 2006, 09:34
:stupid_in désolé j'avais pas vu qu'il fallait te l'expliquer en 2 mots. :ptdr: :ptdr: :ptdr:
Bon si jamais quelqu'un relève ce défi je veux bien lui payer un coup !!!!
Bon si jamais quelqu'un relève ce défi je veux bien lui payer un coup !!!!
par math* » 17 Déc 2006, 09:34
Bonjour,
Il faut en fait chercher les points d'intersection de C et de d :
On résout le système :
y=2x²+bx+3
y=x+1
soit en fait :
2x²+bx+3=x+1
Après simplification de cette équtaion, on trouve le discriminant [(b-1)²-16]
Pour qu'il n'y ait qu'un seul point commun, il faut que le discriminant soit nul.
Donc que (b-1)² =16
On en déduit les deux valeurs de b.
Pour qu'il n'y ait aucun point d'intersection, il faut que l'équation n'admette aucune solution, donc que le discriminant soit négatif.
Il faut donc résoudre l'inéquation :
(b-1)²-16<0
Et tu en déduis l'intervalle de valeurs de b pour lesquelles C et d n'ont aucun point en commun.
Il faut en fait chercher les points d'intersection de C et de d :
On résout le système :
y=2x²+bx+3
y=x+1
soit en fait :
2x²+bx+3=x+1
Après simplification de cette équtaion, on trouve le discriminant [(b-1)²-16]
Pour qu'il n'y ait qu'un seul point commun, il faut que le discriminant soit nul.
Donc que (b-1)² =16
On en déduit les deux valeurs de b.
Pour qu'il n'y ait aucun point d'intersection, il faut que l'équation n'admette aucune solution, donc que le discriminant soit négatif.
Il faut donc résoudre l'inéquation :
(b-1)²-16<0
Et tu en déduis l'intervalle de valeurs de b pour lesquelles C et d n'ont aucun point en commun.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :