Exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 19:27
par anima » 13 Déc 2006, 19:27
amar21 a écrit:j'ai une question tu vois quand on fait la derivée on trouve e^x * (1-x) donc apres le tableau de variation c'est du signe de (1-x) et je fais les variations donc j'obitens la variation mais il me disent dresser le tableau de variation de f(x) je laise comme il est avec la variation de (1-x) ou pas?? ils demandent etudier le sens de variation de f puis dresser son tableau de variatio donc je laisse comme jai fais ou pas??
Bah oui. e^x est toujours positif :we:
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Déc 2006, 19:41
par fonfon » 13 Déc 2006, 19:41
je n'ai rien à ajouter à ce qu'a dit anima
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:50
par amar21 » 13 Déc 2006, 19:50
anima a écrit:Bah oui. e^x est toujours positif :we:
merci a tous les 2
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 20:02
par amar21 » 13 Déc 2006, 20:02
jai un autre rtruc a demander dans le sujet de juin 2005 natinal ils nous disent d'etudier les variations de la fonction f donc jai fais la derivée0 et j'obtiens 1/2 e^-x/4 tout ca divisé par (1+2(e^-x/4)) multiplié par 3 au numerateur et la fonction c'est f(x)= 3 / 1+2e^-x/4 .
une fois que jai fais la derivée comment je fais pour la tableau de variation ??
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 20:06
par anima » 13 Déc 2006, 20:06
amar21 a écrit:jai un autre rtruc a demander dans le sujet de juin 2005 natinal ils nous disent d'etudier les variations de la fonction f donc jai fais la derivée0 et j'obtiens 1/2 e^-x/4 tout ca divisé par (1+2(e^-x/4)) multiplié par 3 au numerateur et la fonction c'est f(x)= 3 / 1+2e^-x/4 .
une fois que jai fais la derivée comment je fais pour la tableau de variation ??
Tu résouds f'(x)=0 puis f'(x) >= 0. Ca te donnera quand f(x) stagne et croit. De là, tu fais ton tableau

P.S.: tu veux bien m'écrire la dérivée avec LaTeX? :zen:
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 20:15
par amar21 » 13 Déc 2006, 20:15
anima a écrit:Tu résouds f'(x)=0 puis f'(x) >= 0. Ca te donnera quand f(x) stagne et croit. De là, tu fais ton tableau

P.S.: tu veux bien m'écrire la dérivée avec LaTeX? :zen:
la dérivée est : f'(x)= ((1/2(e^-x/4)*3)/(1+2(e^-x/4))^2 voila la dérivée
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 20:17
par amar21 » 13 Déc 2006, 20:17
comment je fais pour la tableau je sais pas comment faire tu peux me donner les variations rapidment parce que moi je pense que comme ya exponentielle au numerateur et denominateur donc il reste que le 3 elle stagne??
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 20:19
par anima » 13 Déc 2006, 20:19
amar21 a écrit:la dérivée est : f'(x)= ((1/2(e^-x/4)*3)/(1+2(e^-x/4))^2 voila la dérivée
=\frac{\frac{3}{2}e^{-x/4}}{(1+2(e^{-x/4})^2})
disions nous
f'(x) sera toujours différente de zéro, pour la simple et bonne raison que le numérateur ne peut pas s'annuler.
f'(x) >= 0 ssi e^(-x/4) >=0 -> vrai pour tout x appartenant à R
Ta dérivée est donc positive sur R, et ta fonction strictement croissante
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 20:22
par amar21 » 13 Déc 2006, 20:22
anima a écrit:=\frac{\frac{3}{2}e^{-x/4}}{(1+2(e^{-x/4})^2})
disions nous
f'(x) sera toujours différente de zéro, pour la simple et bonne raison que le numérateur ne peut pas s'annuler.
f'(x) >= 0 ssi e^(-x/4) >=0 -> vrai pour tout x appartenant à R
Ta dérivée est donc positive sur R, et ta fonction strictement croissante
ok merci et le tableau pas besoin de le faire ca suffit je pense
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 20:49
par amar21 » 13 Déc 2006, 20:49
dsl de te dernager encore mais j'ai une exo sur les suites on a U1=1/3 et Un+1= n+1/3n et le numerateur multiplié par Un. on me demande de calculer U2, U3,U4 et pour nsuperieur ou egal a 1 vn= Un/n et on me demande de montrer que la suite est geometrique et preciser sa raison et en deduire Un en fonction de n. on me demande aussi de donner le sens de variation de la suite (Vn) et enfin montrer qu'à partir d'un certain rang la suite (Un) est monotone. est ce que quelqu'un peut m'aider a resoudre cet exercice ?
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 20:51
par anima » 13 Déc 2006, 20:51
amar21 a écrit:dsl de te dernager encore mais j'ai une exo sur les suites on a U1=1/3 et Un+1= n+1/3n et le numerateur multiplié par Un. on me demande de calculer U2, U3,U4 et pour nsuperieur ou egal a 1 vn= Un/n et on me demande de montrer que la suite est geometrique et preciser sa raison et en deduire Un en fonction de n. on me demande aussi de donner le sens de variation de la suite (Vn) et enfin montrer qu'à partir d'un certain rang la suite (Un) est monotone. est ce que quelqu'un peut m'aider a resoudre cet exercice ?
Je n'ai jamais aimé les suites, donc ca ne sera sûrement pas moi.
P.S.: Un petit conseil, la balise TEX est ta meilleure amie pour écrire les équations maths. Apprends à l'utiliser et écris tes formules avec, c'est
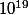
fois plus lisible
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 14 Déc 2006, 10:32
par fonfon » 14 Déc 2006, 10:32
Salut,
pour l'exo sur les suites est-ce que c'est:
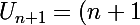\times\frac{u_n}{3n})
si c'est ça pour montrer que Vn est geometrique calcule

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 90 invités
