Exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 18:46
par amar21 » 13 Déc 2006, 18:46
quelle est l'equation de la tangente avec f(x)=(x)/((e^x)-x) et la derivée est f'(x)= (e^x)(1-x) tout ca divisé par ((e^x)-x)^2 la tangente c'est en 0
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 18:51
par anima » 13 Déc 2006, 18:51
amar21 a écrit:quelle est l'equation de la tangente avec f(x)=(x)/((e^x)-x) et la derivée est f'(x)= (e^x)(1-x) tout ca divisé par ((e^x)-x)^2 la tangente c'est en 0
Tu t'es planté dans ta dérivée. Je trouve:
 = \frac{e^x(1-x)-2x}{(e^x-x)^2})
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Déc 2006, 18:52
par fonfon » 13 Déc 2006, 18:52
salut,
tu as
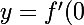(x-0)+f(0))
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 18:53
par amar21 » 13 Déc 2006, 18:53
non je me suis pas trompé verifie bien ya un + qui rentre
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 18:54
par amar21 » 13 Déc 2006, 18:54
fonfon a écrit:salut,
tu as
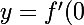(x-0)+f(0))
oui mais en remplacant tout j'obrtiens x c'est normal??
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 18:55
par anima » 13 Déc 2006, 18:55
amar21 a écrit:non je me suis pas trompé verifie bien ya un + qui rentre
}{v(x)}}{dx} = \frac{u'(x)v(x) - v'(x)u(x)}{v^2(x)})
As-tu appliqué cette formule? :triste:
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Déc 2006, 18:55
par fonfon » 13 Déc 2006, 18:55
anima a écrit:Tu t'es planté dans ta dérivée. Je trouve:
 = \frac{e^x(1-x)-2x}{(e^x-x)^2})
moi,je trouve bien
=\frac{(1-x)e^x}{(e^x-x)^2})
-
anima
- Membre Transcendant
- Messages: 3762
- Enregistré le: 15 Sep 2006, 11:00
-
 par anima » 13 Déc 2006, 18:56
par anima » 13 Déc 2006, 18:56
fonfon a écrit:moi,je trouve bien
=\frac{(1-x)e^x}{(e^x-x)^2})
Ok. J'ai du me planter qqpart :hum:
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 18:56
par amar21 » 13 Déc 2006, 18:56
anima a écrit:}{v(x)}}{dx} = \frac{u'(x)v(x) - v'(x)u(x)}{v^2(x)})
As-tu appliqué cette formule? :triste:
oui recalcule tu verras
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Déc 2006, 18:57
par fonfon » 13 Déc 2006, 18:57
oui mais en remplacant tout j'obrtiens x c'est normal??
oui, il n'y a rien de bizarre c'est le bon resultat
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 18:58
par amar21 » 13 Déc 2006, 18:58
et pour le calcul de la tangente on obtient quoi s'il vous plait j'obtiens x c'est noemal??
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 18:59
par amar21 » 13 Déc 2006, 18:59
fonfon a écrit:oui, il n'y a rien de bizarre c'est le bon resultat
ok merci et quand ils disent etudier les postions relatives entre f(x) et la tangente vous ontenez quoi??
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:05
par amar21 » 13 Déc 2006, 19:05
amar21 a écrit:ok merci et quand ils disent etudier les postions relatives entre f(x) et la tangente vous ontenez quoi??
et il me demande de m'aider de la partie a avec g(x)= e^x-x-1 et jai determiné sa variation et la derivée et tout
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Déc 2006, 19:08
par fonfon » 13 Déc 2006, 19:08
il faut que tu études le signe de f(x)-x quand c'est >0 alors la courbe est au dessus de la tangente, quand c'est <0 alors la courbe est au dessous de la tangente
oui alors tu utilises le fait que:
}-x=\frac{-xg(x)}{e^x-x})
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:13
par amar21 » 13 Déc 2006, 19:13
fonfon a écrit:il faut que tu études le signe de f(x)-x quand c'est >0 alors la courbe est au dessus de la tangente, quand c'est <0 alors la courbe est au dessous de la tangente
oui alors tu utilises le fait que:
}-x=\frac{-xg(x)}{e^x-x})
oui mais comment on repond a la keqtion il demande a l'aide de la partie a c'est g(x) etudier la position de la courbe de f(x) par rapport a la tangente
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:16
par amar21 » 13 Déc 2006, 19:16
fonfon a écrit:il faut que tu études le signe de f(x)-x quand c'est >0 alors la courbe est au dessus de la tangente, quand c'est <0 alors la courbe est au dessous de la tangente
oui alors tu utilises le fait que:
}-x=\frac{-xg(x)}{e^x-x})
est-ce que je fais un tableau avec les variations de g(x) et les variation de -x et je dis a la derniere colonne les positions ?
-
fonfon
- Membre Transcendant
- Messages: 5451
- Enregistré le: 18 Oct 2005, 07:53
-
 par fonfon » 13 Déc 2006, 19:17
par fonfon » 13 Déc 2006, 19:17
tu as dû montrer que g(x)>=0 sur R donc f(x)-x est du signe de -x sur ton ensemble de definition
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:19
par amar21 » 13 Déc 2006, 19:19
fonfon a écrit:tu as dû montrer que g(x)>=0 sur R donc f(x)-x est du signe de -x sur ton ensemble de definition
oui donc je fais que les variation de -x c'est ca??
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:23
par amar21 » 13 Déc 2006, 19:23
amar21 a écrit:oui donc je fais que les variation de -x c'est ca??
c'est ce que j'ai fais et ca marche bien
-
amar21
- Membre Naturel
- Messages: 29
- Enregistré le: 13 Déc 2006, 18:41
-
 par amar21 » 13 Déc 2006, 19:25
par amar21 » 13 Déc 2006, 19:25
j'ai une question tu vois quand on fait la derivée on trouve e^x * (1-x) donc apres le tableau de variation c'est du signe de (1-x) et je fais les variations donc j'obitens la variation mais il me disent dresser le tableau de variation de f(x) je laise comme il est avec la variation de (1-x) ou pas?? ils demandent etudier le sens de variation de f puis dresser son tableau de variatio donc je laisse comme jai fais ou pas??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
