Bonjour,
je suis en terminale avec spé mathématiques.
j'ai mon grand oral dans deux jours mais je ne comprends toujours pas quelque chose.
pourquoi ln(1+t) ≈ t ?
si quelqu'un peut m'aider...
merci d'avance
Logarithme
14 messages
- Page 1 sur 1
Re: logarithme
Bonjour,
Tel quel, sans conditions ... c'est faux.
Cette approximation n'est vraie que pour t aux alentours de 0
Tel quel, sans conditions ... c'est faux.
Cette approximation n'est vraie que pour t aux alentours de 0
Re: logarithme
J'ai envie de répondre par une autre question :
Sais-tu pourquoi sin(t)≈t ? (avec les même réserves que ce que disait Black Jack bien entendu)
Sais-tu pourquoi exp(t)≈1+t ? (avec les même réserves que ce que disait Black Jack bien entendu)
Etc etc
As-tu en tête une fonction, et une propriété de ce genre, où tu as compris pourquoi on peut faire l'approximation ?
Si tu sais pourquoi c'est vrai dans les 2 cas ci-dessus, alors tu as pratiquement la réponse à ta question.
Si tu ne sais pas pourquoi c'est vrai dans ces 2 cas, alors on a une piste pour savoir où est le chainon manquant.
Sais-tu pourquoi sin(t)≈t ? (avec les même réserves que ce que disait Black Jack bien entendu)
Sais-tu pourquoi exp(t)≈1+t ? (avec les même réserves que ce que disait Black Jack bien entendu)
Etc etc
As-tu en tête une fonction, et une propriété de ce genre, où tu as compris pourquoi on peut faire l'approximation ?
Si tu sais pourquoi c'est vrai dans les 2 cas ci-dessus, alors tu as pratiquement la réponse à ta question.
Si tu ne sais pas pourquoi c'est vrai dans ces 2 cas, alors on a une piste pour savoir où est le chainon manquant.
Re: logarithme
A noter toutefois : au lycée, on ne fait pas ces approximations (on ne voit pas les développements limites, les équivalences, etc.).
Par contre, quand on dit "t proche de zéro", cela signifie concrètement que "t tend vers zéro".
Donc indication : si vous divisez par t, vous obtenez quelle approximation ?
Or la fraction obtenue vous fait penser à quelle notion du programme que vous avez vue en première ?
Par contre, quand on dit "t proche de zéro", cela signifie concrètement que "t tend vers zéro".
Donc indication : si vous divisez par t, vous obtenez quelle approximation ?
Or la fraction obtenue vous fait penser à quelle notion du programme que vous avez vue en première ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: logarithme
bonsoir,
on va expliquer ce qu'est la meilleure approximation affine
Considérons une fonction définie dans un voisinage de a (a réel) et dérivable en a:
on a
-f(a)}{x-a}=f'(a))
d'où
-f(a)}{x-a}-f'(a) \right)=0)
donc la fonction , notée epsilon , définie par
= \dfrac{f(x)-f(a)}{x-a}-f'(a)) a pour limite zéro quand x tend vers a.
a pour limite zéro quand x tend vers a.
d'où , de= \dfrac{f(x)-f(a)}{x-a}-f'(a))
on tire , en multipliant les deux membres de l'égalité par x-a,
(x-a)= f(x)-f(a)-f'(a)(x-a))
d"où=f(a)+f'(a)(x-a)+\epsilon(x) (x-a))
l'expression+f'(a)(x-a)) est une fonction affine de la variable x et elle approche f(x)
est une fonction affine de la variable x et elle approche f(x)
quand x tend vers a.
on note
 \sim f(a)+f'(a)(x-a)) en négligeant le terme
en négligeant le terme  (x-a)) qui tend "doublement" vers zéro
qui tend "doublement" vers zéro
application
en posant et
et 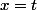 , il vient
, il vient
\sim f(0)+f'(0)t)
\sim exp(0)+exp(0)t \sim 1+t)

 \sim Ln(1)+\dfrac{1}{1+0}t \sim t)
 \sim sin(0)+cos(0)t\sim t)
 \sim cos(0)-sin(0)t \sim 1)
on va expliquer ce qu'est la meilleure approximation affine
Considérons une fonction définie dans un voisinage de a (a réel) et dérivable en a:
on a
d'où
donc la fonction , notée epsilon , définie par
d'où , de
on tire , en multipliant les deux membres de l'égalité par x-a,
d"où
l'expression
quand x tend vers a.
on note
application
en posant
Modifié en dernier par mathelot le 21 Juin 2021, 22:03, modifié 1 fois.
Re: logarithme
Black Jack a écrit:Bonjour,
Tel quel, sans conditions ... c'est faux.
Cette approximation n'est vraie que pour t aux alentours de 0
Oui en effet dans mon exercice t est compris entre 0 et 0,1
merci
Re: logarithme
lyceen95 a écrit:J'ai envie de répondre par une autre question :
Sais-tu pourquoi sin(t)≈t ? (avec les même réserves que ce que disait Black Jack bien entendu)
Sais-tu pourquoi exp(t)≈1+t ? (avec les même réserves que ce que disait Black Jack bien entendu)
Etc etc
As-tu en tête une fonction, et une propriété de ce genre, où tu as compris pourquoi on peut faire l'approximation ?
Si tu sais pourquoi c'est vrai dans les 2 cas ci-dessus, alors tu as pratiquement la réponse à ta question.
Si tu ne sais pas pourquoi c'est vrai dans ces 2 cas, alors on a une piste pour savoir où est le chainon manquant.
D'accord merci je vais réfléchir à partir de cela
Re: logarithme
hdci a écrit:A noter toutefois : au lycée, on ne fait pas ces approximations (on ne voit pas les développements limites, les équivalences, etc.).
Par contre, quand on dit "t proche de zéro", cela signifie concrètement que "t tend vers zéro".
Donc indication : si vous divisez par t, vous obtenez quelle approximation ?
Or la fraction obtenue vous fait penser à quelle notion du programme que vous avez vue en première ?
On obtient ln(1+t)/t ≈ t/t donc 1
et si on fais la limite on a lim t->0 ln(1+t)/t = 1
les deux concordent. est-ce bien ça ?
merci beaucoup !
Re: logarithme
Eula a écrit:On obtient ln(1+t)/t ≈ t/t donc 1
et si on fais la limite on a lim t->0 ln(1+t)/t = 1
les deux concordent. est-ce bien ça ?
merci beaucoup !
Attention à ne pas inverser le raisonnement : montrer que ln(1+t) est proche de t, cela revient à montrer que ln(1+t)/t est proche de 1.
Mais pourquoi ln(1+t)/t est-il proche de 1 ? Autrement dit, pourquoi lim(ln(1+t)/t)=1 ?
Il faut donner un argument ici, et cet argument a trait à une notion vue en première, la même d'ailleurs que celle décrite par mathelot et par catamat.
Si vous ne "voyez" pas, remplacez alors la lettre t par la lettre h, car c'est sûrement avec un "h" que vous avez vu la définition de cette notion en première.
Et si vous ne voyez toujours pas, écrivez ln(1+h)/h = (ln(1+h)-ln(1))/h : quand h tend vers zéro, le résultat est... ?
(PS : pour sin(t), e^t-1 etc. c'est exactement le même raisonnement.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: logarithme
mathelot a écrit:bonsoir,
on va expliquer ce qu'est la meilleure approximation affine
Considérons une fonction définie dans un voisinage de a (a réel) et dérivable en a:
on a
d'où
donc la fonction , notée epsilon , définie para pour limite zéro quand x tend vers a.
d'où , de
on tire , en multipliant les deux membres de l'égalité par x-a,
d"où
l'expressionest une fonction affine de la variable x et elle approche f(x)
quand x tend vers a.
on noteen négligeant le terme
qui tend "doublement" vers zéro
application
en posantet
, il vient
Merci beaucoup pour cette super explication !!
Cela me semble plus clair
Re: logarithme
hdci a écrit:Eula a écrit:On obtient ln(1+t)/t ≈ t/t donc 1
et si on fais la limite on a lim t->0 ln(1+t)/t = 1
les deux concordent. est-ce bien ça ?
merci beaucoup !
Attention à ne pas inverser le raisonnement : montrer que ln(1+t) est proche de t, cela revient à montrer que ln(1+t)/t est proche de 1.
Mais pourquoi ln(1+t)/t est-il proche de 1 ? Autrement dit, pourquoi lim(ln(1+t)/t)=1 ?
Il faut donner un argument ici, et cet argument a trait à une notion vue en première, la même d'ailleurs que celle décrite par mathelot et par catamat.
Si vous ne "voyez" pas, remplacez alors la lettre t par la lettre h, car c'est sûrement avec un "h" que vous avez vu la définition de cette notion en première.
Et si vous ne voyez toujours pas, écrivez ln(1+h)/h = (ln(1+h)-ln(1))/h : quand h tend vers zéro, le résultat est... ?
(PS : pour sin(t), e^t-1 etc. c'est exactement le même raisonnement.
la limite de (ln(1+h)-ln(1))/h quand h tend vers zéro est de 1 . car (f(a+h)-f(a))/ h =f'(a) donc ici ln'(1)=1/1=1
dans mon exercice ln(1+h) ≈ h, tout est multiplié par h !
merci !!
Re: logarithme
Quand 2 nombres sont égaux, si on les multiplie par h, les nombres obtenus sont égaux aussi.
Quand 2 nombres sont presque égaux, si on les multiplie par h, les nombres obtenus sont presque égaux aussi.
Donc, si dans ton exercice tout est multiplié par h, ce n'est pas une erreur ni un problème...
Quand 2 nombres sont presque égaux, si on les multiplie par h, les nombres obtenus sont presque égaux aussi.
Donc, si dans ton exercice tout est multiplié par h, ce n'est pas une erreur ni un problème...
Re: logarithme
Bonjour,
L'important quand on écrit \sim g(t)) quand t tend vers zéro,ce n'est pas que les fonctions soient proches l'une de l'autre mais qu'elles soient équivalentes dans la recherche de limite de produits ou de quotients, i. e,, que l'on puisse les échanger, les intervertir.
quand t tend vers zéro,ce n'est pas que les fonctions soient proches l'une de l'autre mais qu'elles soient équivalentes dans la recherche de limite de produits ou de quotients, i. e,, que l'on puisse les échanger, les intervertir.
L'important quand on écrit
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 92 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

