[ Résolu !!! ] Exponentielle

[haricot29]

pour la suestion 2 c:
il faut montrer que la lim de (f(x) - d) = 0 qd x tend ver +infini
f(x) - d = (-xe^x) / (e^x +1)
lim (-xe^x) / (e^x +1) = lim -x / (1+1/e^x) qd x tend vers +infini
mais je trouve une forme du type -infini /1 c'est pas logique ? il faut que je trouve lim =0 ???!!!
:briques:

[Elsa_toup]

Bonjour,

Ta dérivée est fausse.
Tu écris:

v(x):e^x +1
v'(x):xe^x

En fait ...
Donc il y a un x en trop.
.

Pour la limite par contre, avec l'asymptote, j'avoue que je trouve comme toi, donc je suis perplexe....
Tu es sûr que tu as bien recopié l'énoncé ? C'est la bonne équation de (d) ?

[fonfon]

Salut, il ne faut pas etudier seumlement la limite de f(x)-(x+2) en +inf et si tu regardais quand x->-inf

[haricot29]

Coucou...
oui c'est ok pour la question 2/c/ j'ai regarder la limitie en -infini et je trouve quelque chose du type : 0/1 donc limf(x)-(d) = 0 qd x tend ver -infini

pour la 3)a)
qd j'ai la dérivée pour faire le tableau de variation :
e^x --> positif sur R
(1+x) --> négatif sur ]-infini ; -1[ ; positif sur ]-1 ; +infini [

donc f'x) doit etre négatif sur ]-infini ; -1[ et positif sur ]-1 ; +infini[
Sauf que probleme sur ma calculatrice ma fonction f'(x) est postive sur -infini ; + infini ???!!!!
:hein: :hein: :hein:

[haricot29]

Hummmm pour la question 3)b) je vois pas du tout comment qui faut faire ?
:help:

[haricot29]

Alors j'ai remis mon nez dans cet exercice...
ds la question 3) a) qd on dérive la fonction f on trouve
f '(x) = (e^x (1-x) +1) / (e^x+1)²
on peut remarquer que f '(x) = g(x) / (e^x+1)²
Il faut montrer que la dérivée de f a meme signe que g
Cela semble logique puisque (e^x+1)² est toujours positive... mais je ne vois pas comment rédiger ? faut il que je fasse un tableau de signe en y introduisant g ?
:hein: :hein:

[quiquoi]

Alors j'ai remis mon nez dans cet exercice...
ds la question 3) a) qd on dérive la fonction f on trouve
f '(x) = (e^x (1-x) +1) / (e^x+1)²
on peut remarquer que f '(x) = g(x) / (e^x+1)²
Il faut montrer que la dérivée de f a meme signe que g
Cela semble logique puisque (e^x+1)² est toujours positive... mais je ne vois pas comment rédiger ? faut il que je fasse un tableau de signe en y introduisant g ?
:hein: :hein:

oui faut faire un tableau de signes ensuite tu dis que en divisant g(x) par une positive ds la derniere ligne de ton tableau de signes, alors g(x) positive et g(x)=f(x)

pour etre plus clair, en divisanr une fonction par une parabole positive, alors g(x) sera toujours positif donc f(x)=g(x)

[haricot29]

dc je fé un tableau avec ds la :
1ere ligne g(x)
2eme ligne (e^x+1)² qui est tjrs positif
dc 3eme ligne : f'(x) meme signe que g(x) c'est ça ?

Par contre pour la question b) je vois pas du tt comment faire....

[quiquoi]

dc je fé un tableau avec ds la :
1ere ligne g(x)
2eme ligne (e^x+1)² qui est tjrs positif
dc 3eme ligne : f'(x) meme signe que g(x) c'est ça ?

Par contre pour la question b) je vois pas du tt comment faire....

non

1ere ligne g(x)
2eme ligne (e^x+1)² qui est tjrs positif
3eme ligne : g(x)/(e^x+1)²
et ensuite ds la derniere ligne tu prouve que f(x)= g(x) dans l'intervalle
S={...}

[haricot29]

S= {a}
avec g(0)=a

mais je ne dois pas trouver f(x)=g(x), la question c'est juste montrer que g a meme signe que la dérivée de f dc c'est ok ?

C'est ok... Yes ?!

[quiquoi]

voui :zen:

[haricot29]

Ok par contre pour la )b) je n'ai aucune idée de comment faire pour trouver p et q ?!!

[quiquoi]

Ok par contre pour la )b) je n'ai aucune idée de comment faire pour trouver p et q ?!!

redonne ta quetion

[quiquoi]

jai relu la question mais je ne sais pas du tout ...dsl... aucune idee ptet que tu devrais factoriser...mais en fait je sais pas dsl :dodo:

[Elsa_toup]

Bonsoir,

En fait, c'est le "a" de la partie A, donc tel que g(a) = 0.
Or f '(x) = .
Donc g(x) = f '(x) (+1)².

Donc g(a) = f '(a) (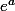+1)² = 0.

Donc f '(a) = 0.
Or f '(a) = =0.
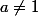Donc , soit , donc . (il faut juste avoir , mais la partie A nous dit que c'est le cas)

Et .

Donc on a bien f(a) = pa+q, avec p = 1 et q = 1.
C'est clair ?

[haricot29]

oui ok merci beaucoup, j'avais commencé comme ça mais je bloquer a un moment donné ( une erreur de signe... Grrr)

[haricot29]

Partie B : Etude de la fonction f

soit f la fonction définie par f(x) = (x/e^x +1)+2
On désigne par (Cf) la courbe representative de f ds un repere orthogonal (O, I, J), unité graph 1 cm pr l'axe des abscisses, 2 cm pr l'axe des ordonnées

1) déterminer la limite de f en +infini et interpréter graph ce résultat.

2)
a) determiner la limite de f en - infini.
b) démontrer que la droite (d) d'éq y=x+2 est une asymptote pr (Cf).
c) etudier la position de Cf par rapport à (d).

3)
a) montrer que la fonction dérivée de f à meme signe que la fonction g [COLOR=Red]etudiée ds la partie A.
b) montrer qu'il existe 2 entiers p et q tel que f(a) = pa + q[/COLOR]
c) dresser le tableau de variation de la fonction f.

4) tracer la courbe (Cf) ds le repere avec ses asymptotes et sa tangente au point d'abscisse a.

Questions en rouge = Questions répondues

[haricot29]

comment je fais pour la question 3)c) car f(x)= x+1
tableau de variations :
f'(x) = 1 toujours positif
dc f(x) strcitement croissante sur R est s'annule en -1
lim f(x) en -infini = -infini
lim f(x) en +infini = + infini

C'est ok ça pour la question 3 c) ??!
:marteau:

[Elsa_toup]

Non, non.
On veut les variations de f(x), pas de f(a).
Il faut que tu reprennes les expressions précédentes de dérivée de f(x).
f ' est du signe de g, donc il faut que tu voies par rapport à ça.

[haricot29]

a ok je reprend ce que j'ai trouver pour f(x) a la question 3)a) est je men sert pour faire mon tableau de variation !