Bonjour à tous,
Notre professeur de maths nous a donné un devoir maison et à vrai dire, je bloque un peu à 2 questions..
Voici l'énoncé :
Un détecteur de faux billet est constitué d'une lampe qui s'allume en bleu lorsque le détecteur considère que le billet testé est vrai, et en rouge lorsqu'il considère que le billet est faux . On note F l'événement : « Le billet testé est faux » et B l'événement: « La lumière qui s'allume est bleue ». Le détecteur n'étant pas infaillible, il se peut qu'il commette des erreurs de détection. On estime que la probabilité qu'un billet soit vrai sachant que la lumière bleue s'est allumée est égale à 95 % et que la probabilité qu'un billet soit faux sachant que la lumière rouge s'est allumée est égale à 95 %.
3a. On note p la probabilité que qu'un billet soit faux. Montrer que :
P(B) = 0.95 - p/0.9
3b. En déduire que 0.05≤ P ≤ 0.95
4. Monter que :
Pf(B) = 0.95 - p/18p
J'ai essayé de chercher et j'ai ça pour le moment :
3a. P(F) = P(F ∩ B) + P ( F ∩ B barre ) = 0.05P(B)+0.95(1-P(B))
Cependant, ça ne ressemble pas à ce qui est indiqué dans l'énoncé. Plus précisément, ce qui me perturbe c'est le "-p" et le dénominateur car je ne vois pas d'où ils peuvent venir.
Merci d'avance pour votre aide !
DM probabilité
5 messages
- Page 1 sur 1
Re: DM probabilité
Bonsoir,
Ne manque-t-il pas des parenthèses ?
Car
me semble correct, et en disant P(F)=p et en développant un peu à droite, cela donne
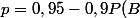)
Ce qui ressemble furieusement à P(B)=(0,95-p)/0,9, avec les parenthèses.
S0nneM0nd a écrit:P(B) = 0.95 - p/0.9
Ne manque-t-il pas des parenthèses ?
Car
S0nneM0nd a écrit:3a. P(F) = P(F ∩ B) + P ( F ∩ B barre ) = 0.05P(B)+0.95(1-P(B))
me semble correct, et en disant P(F)=p et en développant un peu à droite, cela donne
Ce qui ressemble furieusement à P(B)=(0,95-p)/0,9, avec les parenthèses.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM probabilité
hdci a écrit:Bonsoir,S0nneM0nd a écrit:P(B) = 0.95 - p/0.9
Ne manque-t-il pas des parenthèses ?
CarS0nneM0nd a écrit:3a. P(F) = P(F ∩ B) + P ( F ∩ B barre ) = 0.05P(B)+0.95(1-P(B))
me semble correct, et en disant P(F)=p et en développant un peu à droite, cela donne
Ce qui ressemble furieusement à P(B)=(0,95-p)/0,9, avec les parenthèses.
Ah oui, il me semble ! Pardonnez-moi, c'est bien P(B) = (0.95-p)/0.9
Justement, je suis un peu perdue à cette étape.. Je vois pas comment développer ça..
Re: DM probabilité
Il n'y a rien à développer.
On vous demande de démontrer que
=\dfrac{0,95-p}{0,9})
Vous avez trouvé
=0,05P(B)+0,95(1-P(B)))
L'énoncé vous dit
Donc=p) , êtes-vous d'accord ?
, êtes-vous d'accord ?
Partant de là ce que vous avez trouvé est
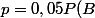+0,95(1-P(B)))
Vous voulez trouver P(B)=...
commencez donc par isoler P(B) d'un côté du signe égal, en faisant les calculs usuels que vous avez appris à faire au collège : c'est-à-dire, commencer par réduire l'expression+0,95(1-P(B))) pour la mettre sous la forme
pour la mettre sous la forme ) où x et y sont deux nombres pas trop durs à calculer.
où x et y sont deux nombres pas trop durs à calculer.
On vous demande de démontrer que
Vous avez trouvé
L'énoncé vous dit
S0nneM0nd a écrit:On note p la probabilité que qu'un billet soit faux
Donc
Partant de là ce que vous avez trouvé est
Vous voulez trouver P(B)=...
commencez donc par isoler P(B) d'un côté du signe égal, en faisant les calculs usuels que vous avez appris à faire au collège : c'est-à-dire, commencer par réduire l'expression
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM probabilité
Bonjour,
Merci, j'ai fini par trouver le résultat ! Cependant pour la 2e je ne suis pas sûre, est ce que je suis sur la bonne route ?
Pour l'instant, j'ai trouvé Pf(B) = P(F ∩B)/P(F) = ((0.95-p)/0.9)* (0.05/( ((0.95-p)/0.9)*0.9)+0.95
Est-ce bon ?
Merci, j'ai fini par trouver le résultat ! Cependant pour la 2e je ne suis pas sûre, est ce que je suis sur la bonne route ?
Pour l'instant, j'ai trouvé Pf(B) = P(F ∩B)/P(F) = ((0.95-p)/0.9)* (0.05/( ((0.95-p)/0.9)*0.9)+0.95
Est-ce bon ?
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
