Démonstration Cauchy-Schartz

[killwin]

Bonjour,

Je ne comprends pas pourquoi cette démonstration de l'inégalité de Cauchy-Schwartz est juste :

On a un espace dans munit du produit scalaire hermitien h. u et v sont des vecteurs.


1) Cas où

démonstration
Je n'écris pas la démonstration, je la comprends

2) Cas où




etc ...

et là pour démontrer on me dit : comme on peut donc choisir le lambda que l'on veut,

on prend


A partir de là je ne comprends pas pourquoi tous les cas possibles sont couverts puisque lambda est lié à u et v ?

Merci d'avance

[zwijndrecht]

Bonjour,
Il y a plusieurs manières de démontrer C.S, mais peut être que l'idée de la preuve est de dire "puisque c'est vrai pour tout lambda, alors, c'est vrai en particulier pour ce lambda-ci".

[killwin]

Du coup, il faudrait démontrer que l'inégalité est vraie pour tous les lambdas non ? J'ai l'impression qu'il manque un bout.

[hdci]

Du coup, il faudrait démontrer que l'inégalité est vraie pour tous les lambdas non ? J'ai l'impression qu'il manque un bout.

Pas du tout.
On dit que est tout le temps vrai (c'est le carré d'un nombre réel...).
Donc elle est vraie pour n'importe quelle valeur de lambda.
En particulier pour
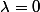
En particulier pour
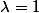
En particulier pour

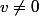
... Et en particulier pour (à condition que toutefois)

Puisqu'elle est vraie pour ce lambda-là (pour les autres on s'en fiche un peu, ils ne seront pas très utiles), et bien regardons ce qui se passe (et c'est la suite de la démonstration)

[killwin]

Merci pour la réponse, je ne savais pas qu'on pouvait démontrer ainsi