Bonjour, je bloque sur cette question :
Soit f une fonction continue de Rn dans Rn, soit a un point de Rn et soit x0=a et x(k+1)=f(xk). Si la suite xk admet une valeur d’adhérence alors elle converge.
Point fixe
11 messages
- Page 1 sur 1
Re: Point fixe
Bonjour,
L'énoncé tel que tu nous le donnes ne va pas. Soit la fonction de
la fonction de  dans
dans  définie par
définie par =1-x) pour tout réel
pour tout réel  . C'est certainement une fonction continue. On considère la suite
. C'est certainement une fonction continue. On considère la suite ) définie par
définie par 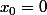 et
et 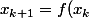) . Cette suite admet 0 comme valeur d'adhérence, mais ne converge pas.
. Cette suite admet 0 comme valeur d'adhérence, mais ne converge pas.
Peut-être ton énoncé dit-il en fait que la suite admet une unique valeur d'adhérence ?
L'énoncé tel que tu nous le donnes ne va pas. Soit
Peut-être ton énoncé dit-il en fait que la suite admet une unique valeur d'adhérence ?
Re: Point fixe
Bien.
Dans la démonstration, l'unicité de la valeur d'adhérence jouera bien sûr un rôle important.
Dans la démonstration, l'unicité de la valeur d'adhérence jouera bien sûr un rôle important.
Re: Point fixe
Ben j'attendais que tu essaies quelque chose, pour éventuellement te donner un coup de pouce.
Une démarche qui devrait venir à l'esprit. Appelons l'unique valeur d'adhérence de la suite. Supposons que
l'unique valeur d'adhérence de la suite. Supposons que ) ne converge pas vers
ne converge pas vers  . On essaie de trouver une contradiction, par exemple en trouvant une seconde valeur d'adhérence.
. On essaie de trouver une contradiction, par exemple en trouvant une seconde valeur d'adhérence.
Une démarche qui devrait venir à l'esprit. Appelons
Re: Point fixe
Pour être honnete je poste pas une question sur internet avant d'avoir essayer moins de 2 heures et typiquement j'ai déjà essayer cette démarche sans succèe. Il se peut que je ne voit pas quelque chose d'évident.
Re: Point fixe
Bonjour,
Je peux te faire un plan de travail :
1°) Montrer que = \ell) . (indice : on peut extraire une suite qui converge vers
. (indice : on peut extraire une suite qui converge vers ) ).
).
On suppose à partir de maintenant que) ne converge pas vers
ne converge pas vers  . Alors il existe un
. Alors il existe un 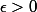 tel qu'il y a une infinité de
tel qu'il y a une infinité de  tels que
tels que  .
.
2°) Montrer qu'il existe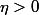 tel qu'il y ait une infinité de
tel qu'il y ait une infinité de  tels que
tels que  (indice : utiliser 1° et la continuité de
(indice : utiliser 1° et la continuité de  ).
).
3°) Conclure.
Je peux te faire un plan de travail :
1°) Montrer que
On suppose à partir de maintenant que
2°) Montrer qu'il existe
3°) Conclure.
Re: Point fixe
J'avais déjà fait la 1 et la 2 je viens simplement de me rappeller de la compacité. Merci.
Re: Point fixe
Si tu avais déjà fait 1 et 2, pourquoi ne l'as-tu pas dit ?
À part écrire que tu as passé deux heures dessus, tu n'as donné aucune indication de recherche que tu aurais déjà faite sur l'exercice. Mets un peu du tien quand tu demandes de l'aide !
À part écrire que tu as passé deux heures dessus, tu n'as donné aucune indication de recherche que tu aurais déjà faite sur l'exercice. Mets un peu du tien quand tu demandes de l'aide !
Re: Point fixe
Oui je le ferais le prochaine fois, j'avais trouvé tellement de choses qui me semblait inutile (qui l'étaient pour la plupart) que je n'ai pas oser faire une liste ici.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
