trouver les entiers relatifs qui vérifient l'inégalité
Inégalité entiers relatifs
9 messages
- Page 1 sur 1
Inégalité entiers relatifs
x,y,z sont des entiers relatifs
trouver les entiers relatifs qui vérifient l'inégalité
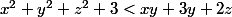
trouver les entiers relatifs qui vérifient l'inégalité
Modifié en dernier par K57 le 05 Déc 2020, 18:26, modifié 5 fois.
Re: Exercice math
bonsoir,
on peut passer tous les termes à gauche du signe < et écrire la décomposition de Gauss d'une forme quadratique, ("forme" veut dire application à valeurs réelles et "quadratique" veut dire de degré 2)
sauf erreur de calculs, on obtient (grâce à la forme canonique d'un trinôme) l'équation équivalente:
^2+3(y-2)^2+4(z-1)^2 < 4)
PS1: on écrit "cet exo" , exo étant du masculin
PS2: deux équations sont équivalentes si elles ont les mêmes solutions
on peut passer tous les termes à gauche du signe < et écrire la décomposition de Gauss d'une forme quadratique, ("forme" veut dire application à valeurs réelles et "quadratique" veut dire de degré 2)
sauf erreur de calculs, on obtient (grâce à la forme canonique d'un trinôme) l'équation équivalente:
PS1: on écrit "cet exo" , exo étant du masculin
PS2: deux équations sont équivalentes si elles ont les mêmes solutions
Re: Exercice math
Bonsoir merci de la reponse, que dois-je faire ensuite ? trouver les solutions ? avec quel formule ?
Re: Exercice math
après, il n'y a plus beaucoup de choix:
par exemple^2) peut seulement prendre la valeur 0.
peut seulement prendre la valeur 0.
par exemple
Modifié en dernier par mathelot le 05 Déc 2020, 19:03, modifié 1 fois.
Re: Exercice math
mathelot a écrit:après, il n'y a plus beaucoup de choix:
par exemplepeut seulement prendre la valeur 0. Au delà,ça dépasse 4.
Tu voulais dire
Re: Exercice math
K57 a écrit:avec quel formule ?
Décidément tu es fâché(e) avec le genre.
Là il faut écrire "quelle formule" car formule est féminin.
Re: a
Bonjour Sa Majesté,
peux tu restaurer l'énoncé du fil qui a été effacé par K57:
x,y,z sont des entiers relatifs
trouver les entiers relatifs qui vérifient l'inégalité
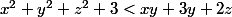
peux tu restaurer l'énoncé du fil qui a été effacé par K57:
x,y,z sont des entiers relatifs
trouver les entiers relatifs qui vérifient l'inégalité
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
