Bonsoir,
Montrons que

,
c'est à dire montrons que
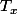
et

ont les mêmes ouverts.
On a montré que
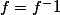
Par conséquent f est bijective (je ne sais pas si j'emploie les bon termes)
c'est-à-dire que tout élément appartenant à

appartient à
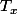
autrement dit tout ouvert de

appartient aussi à
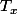
Par conséquent, les deux topologies ont les mêmes ouverts.
(Je ne sais pas si je me suis bien exprimé, vous pouvez me reprendre)
Si f est continue alors l'image réciproque d'un ouvert est ouvert c'est à dire :
pour tout
 \in T_2)
Edit: peut-être dois-je montrer que si f est bijectif et ouvert (ou fermé) alors f est un homéomorphisme ?
