Systeme equation trigonométrique 2 inconnues
7 messages
- Page 1 sur 1
Systeme equation trigonométrique 2 inconnues
par Etudiament » 03 Oct 2020, 09:03
.
Modifié en dernier par Etudiament le 04 Oct 2020, 09:28, modifié 1 fois.
Re: Systeme equation trigonométrique 2 inconnues
par vam » 03 Oct 2020, 09:31
Bonjour
c'est trouver 2 nombres connaissant somme et produit (cela débouche sur une simple équation du second degré)
X=cos(x) et Y=sin(y) si tu veux
c'est trouver 2 nombres connaissant somme et produit (cela débouche sur une simple équation du second degré)
X=cos(x) et Y=sin(y) si tu veux
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Systeme equation trigonométrique 2 inconnues
par Etudiament » 03 Oct 2020, 10:11
C'est à dire je vois pas... parce qu'il y a un sinus dans la deuxième équation, et non un cos...
Re: Systeme equation trigonométrique 2 inconnues
par vam » 03 Oct 2020, 10:36
ah zut, excuse moi, je n'avais pas fait assez attention, désolée
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Systeme equation trigonométrique 2 inconnues
par vam » 03 Oct 2020, 10:48
Une méthode "bête et méchante", consiste à tirer sin(y) de la 1re, à reporter dans la 2e, et tout mettre en fonction de t=tan(x/2)
Sauf erreur de ma part, ça débouche (on trouve les valeurs approchées de t)
Sauf erreur de ma part, ça débouche (on trouve les valeurs approchées de t)
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Systeme equation trigonométrique 2 inconnues
par vam » 03 Oct 2020, 12:31
tu ne vas pas manquer de pistes...http://www.bibmath.net/forums/viewtopic.php?id=12990
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Systeme equation trigonométrique 2 inconnues
par Pisigma » 04 Oct 2020, 08:32
Bonjour,
autre piste pas plus simple!
=1-sin(y) & \\ <br />sin(x)=-\dfrac{3}{4\,sin(y)} & <br />\end{cases})
en élevant au carré et en ajoutant membre à membre , on obtient, sauf erreur
-32\, sin^3(y)+9=0<br /><br />~~(y\ne k\pi))
soit à résoudre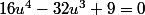
, en posant )
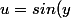à résoudre à l'aide d'une méthode numérique (dichotomie, Newton,...)
autre piste pas plus simple!
en élevant au carré et en ajoutant membre à membre , on obtient, sauf erreur
soit à résoudre
à résoudre à l'aide d'une méthode numérique (dichotomie, Newton,...)
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 59 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :