Relations binaires

[doudia]

Hola,
est ce qu'on peut parler deajorant et de minorant pour des relations d'ordre autre que <= et>= .
Merci!

[doudia]

Je me rends compte que je n'ai pas vraiment bien posé la question , quand on a fait le cours le prof a pris une relation d'ordre quelconque R sur un ensemble E et un element b de E et A une partie de E puis il nous a dit que b est un majorant de A si :pour tout x de A, xRb .
mais quand je prends >= comme relation d'ordre ça me fait tout bizarre d'appeler les plus petits nombres des majorants.

[GaBuZoMeu]

Bonjour,

À partir du moment où tu fais le choix d'un ordre sur un ensemble , il est normal de lire 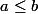comme " est inférieur ou égal à ", non ? (Sous-entendu : pour l'ordre choisi sur .)

[doudia]

Ce n'est toujours pas clair ,si on prend A={2,3,4} on a >= est une relation d'ordre sur IN et 2>=1 3>=1 4>=1 donc d'apres la definition donnée par notre prof 1 est un majorant de A ce qui n'a aucun sens pour moi.
Je suis perdue je veux juste comprendre comment appliquer cette definition mercii!

[GaBuZoMeu]

La définition est claire, non ?

une relation d'ordre quelconque R sur un ensemble E et un element b de E et A une partie de E puis il nous a dit que b est un majorant de A si :pour tout x de A, xRb .

Quand on a une relation d'ordre sur un ensemble , on a l'habitude de la noter plutôt que .
Ce qui te perturbe, c'est que la relation inverse d'une relation d'ordre est aussi une relation d'ordre. Un minorant pour une relation d'ordre donnée est un majorant pour la relation d'ordre inverse, et vice-versa.
Un minorant pour est un majorant pour l'ordre inverse . Bon, faut s'y faire. Mais en fait, on ne travaille pratiquement jamais en même temps avec un ordre et avec l'ordre inverse. On a un ordre bien choisi avec lequel on travaille, et basta !

[doudia]

Aaah d'accord, c'est plus clair maintenant

[tournesol]

Pour moi 1 est un minoŕant de {2,3,4} pour >= et pour <= .
Quand on utilise >= , on doit lire de droite à gauche .

[GaBuZoMeu]

1 n'est pas un minorant de {2,3,4} pour la relation d'ordre 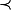sur définie par .

[tournesol]

GaBuSoMeu
Nous sommes bien d'accord qu'un minorant pour une relation d'ordre devient un majorant pour l'ordre inverse .
Moi je parlais de la comparaison usuelle des réels et on écrit alors indifferemment a<=b ou b>=a , mais quand on utilise la deuxieme ecriture (qui se lit supérieur ou égal) , il est entendu qu'elle a la signification de la première mais en lisant de droite à gauche . Quand on dit "5 est superieur a 3" , 3 n'est pas un majorant de 5 ...ou alors je n'ai rien compris à la manipulation des inegalités au collège et au lycée .

[GaBuZoMeu]

Nous sommes bien d'accord qu'un minorant pour une relation d'ordre devient un majorant pour l'ordre inverse .

Très bien, il n'y a donc pas besoin d'en faire toute une histoire et d'embrouiller doudia.