Bonjour pourriez vous m’aider à résoudre le problème suivant :
Avec : a_{n}=(2-2n)/(2n-1)
Justifier : (a_{1}+1)(a_{2}+1)+(a_{2}+1)(a_{3}+1)+...+(a_{n}+1)(a_{n+1}+1) < 1/2
Merci de votre aide !
Petit problème de math
11 messages
- Page 1 sur 1
Re: Petit problème de math
hello
as tu calculé quelques termes de ta justification?
as tu calculé quelques termes de ta justification?
la vie est une fête 
Re: Petit problème de math
fatal_error a écrit:hello
as tu calculé quelques termes de ta justification?
Oui bien sûr :
( a_{1}+1)(a_{2}+1) = 1/3
(a_{2}+1)(a_{3}+1) = 1/15
(a_{n}+1)(a_{n+1}+1) = (1)/[(2_{n}-1)*(2_{n+1}-1)]
Et voilà où j’en suis...
Merci de ton aide
Re: Petit problème de math
peut être voulais tu écrire
... < 1/2 et non > 1/2 alors ?
... < 1/2 et non > 1/2 alors ?
la vie est une fête 
Re: Petit problème de math
fatal_error a écrit:peut être voulais tu écrire
... < 1/2 et non > 1/2 alors ?
A oui c’est exact xD
Re: Petit problème de math
fatal_error a écrit:peut être voulais tu écrire
... < 1/2 et non > 1/2 alors ?
Du coup j’ai réécrit xD désolé pour la faute
Re: Petit problème de math
On a une somme de n termes. On veut montrer que cette somme est inférieure à 1/2.
Si par hasard, chacun des termes de la somme était inférieur à 1/2n, alors ce serait résolu. Est-ce le cas ?
... Non.
Bon, cherchons une 2ème piste.
Pour montrer que cette somme est inférieure à 1/2 , on peut essayer de montrer que 2 fois cette somme est inférieur à 1 (oui je sais , ça a l'air idiot).
Et pour simplifier les écritures et les calculs, je vais définir une autre variable :
On écrit cette somme, dans l'ordre comme dans l'énoncé.
Et en-dessous, on écrit à nouveau la somme, mais en ordonnant les termes dans l'autre ordre.
Et on additionne les termes 2 à 2 : (le premier + le dernier)
(le premier + le dernier)
Puis ( le 2ème + l'avant dernier)
( le 2ème + l'avant dernier)
et de manière générale,
Si on arrive à prouver que chacun de ces termes est inférieur à 1/n , alors c'est bon, on a résolu l'exercice.
est inférieur à 1/n , alors c'est bon, on a résolu l'exercice.
J'ai pu me tromper sur les indices... mais la piste est là.
Si par hasard, chacun des termes de la somme était inférieur à 1/2n, alors ce serait résolu. Est-ce le cas ?
... Non.
Bon, cherchons une 2ème piste.
Pour montrer que cette somme est inférieure à 1/2 , on peut essayer de montrer que 2 fois cette somme est inférieur à 1 (oui je sais , ça a l'air idiot).
Et pour simplifier les écritures et les calculs, je vais définir une autre variable :
On écrit cette somme, dans l'ordre comme dans l'énoncé.
Et en-dessous, on écrit à nouveau la somme, mais en ordonnant les termes dans l'autre ordre.
Et on additionne les termes 2 à 2 :
Puis
et de manière générale,
Si on arrive à prouver que chacun de ces termes
J'ai pu me tromper sur les indices... mais la piste est là.
Re: Petit problème de math
Je pense que c'est pas ce qui est attendu mais on peut calculer bêtement:

-1} = -1 + \frac{1}{2n+1})
d'où(a_{n+1}+1) = \frac{1}{2n-1} \times \frac{1}{2n+1} = \frac{1}{4n^2-1})
Si on pose
Alors on a la récurrence linéaire

La solution est donnée par
 avec
avec 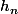 la solution de l'eq homogène
la solution de l'eq homogène  idem
idem 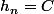 , C une constante
, C une constante
et une solution particulière est donnée par
est donnée par
-1})
Pour fixer C, on impose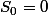 (de sorte que
(de sorte que  )
)
et on obtient

d'où le terme général
)
On a alors pour n > 0,
d'où
Si on pose
Alors on a la récurrence linéaire
La solution est donnée par
et une solution particulière
Pour fixer C, on impose
et on obtient
d'où le terme général
On a alors pour n > 0,
la vie est une fête 
Re: Petit problème de math
Salut,
Pareil que fatal_error jusque (a(n)+1 )*(a(n+1) + 1) = 1/(4n²-1)
On démontre ensuite (classique) que 1/(4n²-1) < 1/(2n) pour tout n >= 1 (simple étude des variations d'une fonction)
Et donc la somme des n termes est < n * (1/(2n))
soit donc < 1/2

Pareil que fatal_error jusque (a(n)+1 )*(a(n+1) + 1) = 1/(4n²-1)
On démontre ensuite (classique) que 1/(4n²-1) < 1/(2n) pour tout n >= 1 (simple étude des variations d'une fonction)
Et donc la somme des n termes est < n * (1/(2n))
soit donc < 1/2
Re: Petit problème de math
fatal_error a écrit:Je pense que c'est pas ce qui est attendu mais on peut calculer bêtement:
d'où
Si on pose
Alors on a la récurrence linéaire
La solution est donnée paravec
la solution de l'eq homogène
idem
, C une constante
et une solution particulièreest donnée par
Pour fixer C, on impose(de sorte que
)
et on obtient
d'où le terme général
On a alors pour n > 0,
Oui, comme tu l’as dit je ne suis pas sûr que c’est la réponse attendue mais merci quand même ! En revanche je n’ai pas compris la partie avec la Constante...
Re: Petit problème de math
Black Jack a écrit:Salut,
Pareil que fatal_error jusque (a(n)+1 )*(a(n+1) + 1) = 1/(4n²-1)
On démontre ensuite (classique) que 1/(4n²-1) < 1/(2n) pour tout n >= 1 (simple étude des variations d'une fonction)
Et donc la somme des n termes est < n * (1/(2n))
soit donc < 1/2
Ah voila je pense que c’est la réponse attendue Mercii a vous trois pour votre aide !
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
