Suite explicitement définie
10 messages
- Page 1 sur 1
Suite explicitement définie
Bonjour, voilà le professeur de mathématiques nous a posé une question assez difficile. Il met la classe au défi de trouver la suite explicitement définie pour laquelle u0=1 ; u1=2 ; u2=3 ; u3=1 ; u4=2 ; u5=3 : u6=1 ; etc.
Re: Suite explicitement définie
Alors, la suite n'est pas bien définie, on pourrait continuer avec par exemple 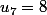 puis
puis 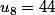 sans qu'aucune logique n'apparaisse. J'imagine que la suite est définie explicitement par
sans qu'aucune logique n'apparaisse. J'imagine que la suite est définie explicitement par  ,
,  et
et  pour tout
pour tout 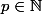 . La suite est périodique de période 3, comme les suites
. La suite est périodique de période 3, comme les suites \right)_{n\in\mathbb{N}}) ,
, \right)_{n\in\mathbb{N}}) et
et _{n\in\mathbb{N}}) . Essaye de trouver
. Essaye de trouver  sous la forme
sous la forme 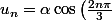+\beta\sin\left(\frac{2n\pi}{3}\right)+\gamma) avec
avec \in\mathbb{R}^3) pour les premiers termes et conclus avec une récurrence.
pour les premiers termes et conclus avec une récurrence.
Re: Suite explicitement définie
On peut aussi trouver une expression en utilisant la fonction partie entière, en particulier E(n/3)
Re: Suite explicitement définie
D’accord, mais alpha, beta et gamma correspondent à quoi dans la formule ?
Re: Suite explicitement définie
C’est à toi de les trouver, en utilisant 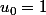 ,
, 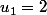 et
et 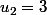 tu as un système d’ordre 3 à résoudre.
tu as un système d’ordre 3 à résoudre.
Re: Suite explicitement définie
D’accord, merci beaucoup de votre aide mais je ne suis encore en première, je n’ai pas encore fait les raisonnements par récurrence
Re: Suite explicitement définie
Ah, sans récurrence ça me parait compliqué, si tu trouves α β et γ, tu peux dire que t’observes que la formule marche bien, si on voulait le prouver je vois pas comment se passer de la récurrence.
Re: Suite explicitement définie
Salut,
Je comprend pas trop à quel endroit tu compte te servir d'une récurrence . . .
Normalement, dés qu'on voit les fonctions numérique (et pas angulaires) sinus et cosinus, on voit qu'elles sont 2.pi-périodique et on en déduit évidement que les suites de terme général sin(2n.pi/3) et cos(2.n.pi/3) sont 3-périodiques.
Je comprend pas trop à quel endroit tu compte te servir d'une récurrence . . .
Normalement, dés qu'on voit les fonctions numérique (et pas angulaires) sinus et cosinus, on voit qu'elles sont 2.pi-périodique et on en déduit évidement que les suites de terme général sin(2n.pi/3) et cos(2.n.pi/3) sont 3-périodiques.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Suite explicitement définie
Revois tes calculs, ça ne marche pas pour u_1. D'ailleurs on peut en effet se passer de récurrence, au temps pour moi, il suffit d'invoquer la périodicité des cos et sin.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
