Notion de partie entière

[Dorcas]

Bonjour aidez-moi s'il vous plaît

Démontrer que pour tout entier k strictement positif:
√k+1-√k<1/2√k<√k-√k-1
En déduire,pour n €N*,la partie entière de la somme:
Sn=somme de k=1 à n^2 de 1/2√k.

[GaBuZoMeu]

Quand on voit une différence de racines carrées , on peut avoir une envie irrépressible de la multiplier par la somme , de façon à trouver ....

[titine]

Bonjour aidez-moi s'il vous plaît

Démontrer que pour tout entier k strictement positif:
√k+1-√k<1/2√k<√k-√k-1
En déduire,pour n €N*,la partie entière de la somme:
Sn=somme de k=1 à n^2 de 1/2√k.

Je ne comprends pas.
√k + 1 - √k = 1
Et √k - √k - 1 = -1
Il faut donc démontrer que 1 < 1/2√k< -1 ????
Vraiment très bizarre ...

[GaBuZoMeu]

Quelques parenthèses manquantes ....

[Dorcas]

Je pense qu'il faut le multiplier par son conjugué,les racines seront alors élevées au carré et donc elles auront disparues.
L'équation obtenue sera égal à 1

[mathelot]

bonsoir,
pour démontrer les deux inégalités, il suffit de multiplier haut et bas les différences
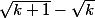et 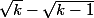(de dénominateurs 1) par leurs quantités conjuguées.