Bonjour, j'ai un travail à rendre en algèbre mais je bloque sur une question, j'ai essayé d'utiliser les formules d'Euler pour lineariser l'inequation mais c'est encore pire. Je ne vois pas comment la résoudre :
cos (5x)+cos(3x) <= cos(x)
Si quelqu'un a une idée de la méthode a utiliser je suis preneur
Merci pour vos futur réponse
Bastien
Inéquations trigonométriques
13 messages
- Page 1 sur 1
Re: Inéquations trigonométriques
Bonjour,
il existe une famille de polynômes, nommés) , dits polynômes de Tchebyshev de 1ère espèce,
, dits polynômes de Tchebyshev de 1ère espèce,
qui vérifient l'égalité suivante:
=T_n(cos(x)))
ie, cos(nx) est un polynôme de la quantité cos(x). n est le degré du polynôme.
https://fr.wikipedia.org/wiki/Polyn%C3% ... Tchebychev
on a:
+cos(3x)-cos(x)=T_5(cos(x))+T_3(cos(x))-T_1(cos(x)))
en posant) , il vient
, il vient
=16z^5-20z^3+5z+4z^3-3z-z \leq 0)
le polynôme en z se factorise en produits de facteurs du 1er degré, en effet:
=16z^5-16z^3+z \leq 0)
=16 z(z^4-z^2+\frac{1}{16}) \leq 0)
on pose (polynôme bi-carré)
(polynôme bi-carré)
 a pour solutions
a pour solutions
 et
et

on a donc:
+cos(3x)-cos(x)=)
 \left(cos(x)-\dfrac{\sqrt{2+\sqrt{3}}}{2}\right)\left(cos(x)+\dfrac{\sqrt{2+\sqrt{3}}}{2}\right)\left(cos(x)-\dfrac{\sqrt{2-\sqrt{3}}}{2}\right)\left(cos(x)+\dfrac{\sqrt{2-\sqrt{3}}}{2}\right))
il existe une famille de polynômes, nommés
qui vérifient l'égalité suivante:
ie, cos(nx) est un polynôme de la quantité cos(x). n est le degré du polynôme.
https://fr.wikipedia.org/wiki/Polyn%C3% ... Tchebychev
on a:
en posant
le polynôme en z se factorise en produits de facteurs du 1er degré, en effet:
on pose
on a donc:
Modifié en dernier par mathelot le 09 Déc 2019, 12:48, modifié 1 fois.
Re: Inéquations trigonométriques
D'accord merci pour la réponse rapide , en revanche je ne connaissais pas cette famille de polynôme.
Re: Inéquations trigonométriques
cos p+cos q= 2cos (p+q)/2 cos(p-q)/2 ton inequation devient
2cos4xcosx cosx soit (cosx)(2cos4x-1)
cosx soit (cosx)(2cos4x-1) 0
0
Il est alors très facile de continuer .
2cos4xcosx
Il est alors très facile de continuer .
Re: Inéquations trigonométriques
Bonjour mathelot , nous travaillons en parallèle .
(cos x )(2cos 4x -1) 0 ssi
0 ssi
[cos x 0 et 2cos 4x-1
0 et 2cos 4x-1 0] ou [cos x
0] ou [cos x 0 et 2cos 4x-1
0 et 2cos 4x-1 0]
0]
ssi il existe k et k' dans Z tels que
[pi/2+2kpi x
x 3pi/2+2kpi et pi/3+2k'pi
3pi/2+2kpi et pi/3+2k'pi 4x
4x 3+2k'pi] ou [-pi/2+2kpi
3+2k'pi] ou [-pi/2+2kpi x
x pi/2+kpi et pi/3+2k'pi
pi/2+kpi et pi/3+2k'pi 4x
4x 5pi/3+2k'pi]
5pi/3+2k'pi]
ssi il existe k et k' dans Z tels que
[pi/2+2kpi x
x 3pi/2+2kpi et pi/12+k'pi/2
3pi/2+2kpi et pi/12+k'pi/2 x
x 12+k'pi/2] ou [-pi/2+2kpi
12+k'pi/2] ou [-pi/2+2kpi x
x pi/2+2kpi et pi/12+k'pi/2
pi/2+2kpi et pi/12+k'pi/2 x
x 5pi/12+k'pi/2]
5pi/12+k'pi/2]
A ce stade il convient de dessiner un cercle trigo gradué en pi/12 pour representer graphiquement les solutions .On obtient:
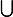 [7pi/12 + 2kpi , 9pi/12+2kpi]
[7pi/12 + 2kpi , 9pi/12+2kpi]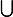
(cos x )(2cos 4x -1)
[cos x
ssi il existe k et k' dans Z tels que
[pi/2+2kpi
ssi il existe k et k' dans Z tels que
[pi/2+2kpi
A ce stade il convient de dessiner un cercle trigo gradué en pi/12 pour representer graphiquement les solutions .On obtient:
Re: Inéquations trigonométriques
SUITE
 [-9pi/12+2kpi,-7pi/12+2kpi]
[-9pi/12+2kpi,-7pi/12+2kpi] 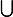
 [7pi/12+2kpi,9pi/12+2kpi]
[7pi/12+2kpi,9pi/12+2kpi] 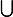
 [-5pi/12+2kpi,-pi/12+2kpi]
[-5pi/12+2kpi,-pi/12+2kpi] 

Re: Inéquations trigonométriques
on range les racines par ordre croissant:
 \left(cos(x)-cos(\dfrac{\pi}{12})\right)\left(cos(x)-cos(\dfrac{5\pi}{12})\right)\left(cos(x)-cos(\dfrac{7\pi}{12})\right)\left(cos(x)-cos(\dfrac{11\pi}{12})\right) \leq 0)
pour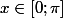
sur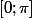 on obtient, si S est l'ensemble de toutes les solutions:
on obtient, si S est l'ensemble de toutes les solutions:

En effet, en x=0, l'inégalité est fausse et ensuite comme les racines sont simples , et que le polynôme est localement monotone au voisinage des racines, le polynôme change de signe au passage de chaque racine.
la fonction étant paire, on complète les solutions par symétrie par rapport à zéro puis par périodicité de période
pour
sur
En effet, en x=0, l'inégalité est fausse et ensuite comme les racines sont simples , et que le polynôme est localement monotone au voisinage des racines, le polynôme change de signe au passage de chaque racine.
la fonction étant paire, on complète les solutions par symétrie par rapport à zéro puis par périodicité de période
Modifié en dernier par mathelot le 09 Déc 2019, 16:13, modifié 2 fois.
Re: Inéquations trigonométriques
Salut,
Il me semble que je n'ai pas les mêmes solutions.
cos(3x) = 4.cos³(x)-3cos(x)
cos(5x) = Re((cos(x) + isin(x)))^5 = cos^5(x) - 10.cos³(x).(1-cos²(x)) + 5.cos(x).(1-cos²(x))²
cos(5x) = cos^5(x) - 10.cos³(x) + 10cos^5(x) + 5.cos(x).(1+cos^4(x)-2cos²(x))
cos(5x) = cos^5(x) - 10.cos³(x) + 10cos^5(x) + 5.cos(x) + 5cos^5(x)- 10cos³(x)
cos(5x) = 16cos^5(x) - 20.cos³(x) + 5.cos(x)
cos(3x) + cos(5x) = 16cos^5(x) - 16.cos³(x) + 2.cos(x)
16cos^5(x) - 16.cos³(x) + 2.cos(x) <= cos(x)
cos(x) = 0 convient,
Si cos(x) diff de 0 --> 16cos^4(x) - 16.cos²(x) + 2 <= 1
16cos^4(x) - 16.cos²(x) + 1 <= 0
Inéquation bicarrée en cos(x) --> facile à résoudre (poser cos²(x) = X)
16X² - 16X + 1 <= 0 (avec X dans ]0 ; 1])
X = [8 +/- V(64 - 16)]/16
X = [8 +/- V48]/16
cos²(x) = [8 +/- 4.V3]/16
cos²(x) = [2 +/- V3]/4
cos(x) = +/-V(2 +/- V3)/2
(cosx) - (2 - V3)/).(cosx) - (4 + V12)/8).(cosx) - (-4 - V12)/8).(cosx) - (-4 + V12)/8) <= 0
(cos(x) - V(2 - V3)/2).(cos(x) - V(2 + V3)/2).(cos(x) + V(2 - V3)/2).(cos(x) + V(2 + V3)/2) <= 0
Tableau de signes ...
- V(2 + V3)/2 <= cos(x) <= - V(2 - V3)/2 OU V(2 - V3)/2 <= cos(x) <= V(2 + V3)/2
x compris dans [Pi/12 ; 5Pi/12] U [Pi/2 ; 7Pi/12] U [11Pi/12 ; Pi] (mod Pi)

Il me semble que je n'ai pas les mêmes solutions.
cos(3x) = 4.cos³(x)-3cos(x)
cos(5x) = Re((cos(x) + isin(x)))^5 = cos^5(x) - 10.cos³(x).(1-cos²(x)) + 5.cos(x).(1-cos²(x))²
cos(5x) = cos^5(x) - 10.cos³(x) + 10cos^5(x) + 5.cos(x).(1+cos^4(x)-2cos²(x))
cos(5x) = cos^5(x) - 10.cos³(x) + 10cos^5(x) + 5.cos(x) + 5cos^5(x)- 10cos³(x)
cos(5x) = 16cos^5(x) - 20.cos³(x) + 5.cos(x)
cos(3x) + cos(5x) = 16cos^5(x) - 16.cos³(x) + 2.cos(x)
16cos^5(x) - 16.cos³(x) + 2.cos(x) <= cos(x)
cos(x) = 0 convient,
Si cos(x) diff de 0 --> 16cos^4(x) - 16.cos²(x) + 2 <= 1
16cos^4(x) - 16.cos²(x) + 1 <= 0
Inéquation bicarrée en cos(x) --> facile à résoudre (poser cos²(x) = X)
16X² - 16X + 1 <= 0 (avec X dans ]0 ; 1])
X = [8 +/- V(64 - 16)]/16
X = [8 +/- V48]/16
cos²(x) = [8 +/- 4.V3]/16
cos²(x) = [2 +/- V3]/4
cos(x) = +/-V(2 +/- V3)/2
(cosx) - (2 - V3)/).(cosx) - (4 + V12)/8).(cosx) - (-4 - V12)/8).(cosx) - (-4 + V12)/8) <= 0
(cos(x) - V(2 - V3)/2).(cos(x) - V(2 + V3)/2).(cos(x) + V(2 - V3)/2).(cos(x) + V(2 + V3)/2) <= 0
Tableau de signes ...
- V(2 + V3)/2 <= cos(x) <= - V(2 - V3)/2 OU V(2 - V3)/2 <= cos(x) <= V(2 + V3)/2
x compris dans [Pi/12 ; 5Pi/12] U [Pi/2 ; 7Pi/12] U [11Pi/12 ; Pi] (mod Pi)
Re: Inéquations trigonométriques
mathelot , je n'ai pas tout à fait les mêmes solutions car je trouve 
Connaissant ta fiabilité , j'ai du commettre une erreur , et une autre car après vérifications je trouve:

Je vais tout reprendre .
Connaissant ta fiabilité , j'ai du commettre une erreur , et une autre car après vérifications je trouve:
Je vais tout reprendre .
Re: Inéquations trigonométriques
tournesol a écrit:mathelot , je n'ai pas tout à fait les mêmes solutions car je trouve
Connaissant ta fiabilité , j'ai du commettre une erreur , et une autre car après vérifications je trouve:
Je vais tout reprendre .
tournesol,pas la peine de reprendre, j'avais oublié la racine pi/2. j'ai corrigé depuis, ce qui fait que je trouve pareil que toi et Black Jack
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
