Division de Polynôme - inéquations difficiles

[maeee]

Bonjour,
mardi je rentre en 1ere année de prépa bcpst et dans mon DM de maths j'ai deux inéquations qui ne sont pourtant pas très difficiles mais sur lesquelles je beugue complétement dessus , pourriez vous m'aider ?

1)
(-2x²+10x-12)/(x²+3x+2) >= 0

2)
{} c'est la valeur absolue:
{2x(x+2)}<={x+3}
Merci d'avance

[Lostounet]

[quote="maeee"]Bonjour,
mardi je rentre en 1ere année de prépa bcpst et dans mon DM de maths j'ai deux inéquations qui ne sont pourtant pas très difficiles mais sur lesquelles je beugue complétement dessus , pourriez vous m'aider ?

1)
(-2x²+10x-12)/(x²+3x+2) >= 0

2)
{} c'est la valeur absolue:
{2x(x+2)} |x - 5|

?

[capitaine nuggets]

Salut !

Posons .
Cherchons alors à écrire sans valeurs absolues :

Etudie, suivant les valeurs du réel , le signe de 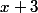, simplifie alors ; fais-en de même avec .

Déduis-en alors, toujours suivant le réel , l'expression de et détermine enfin pour quelles valeurs de a-t-on .

[Black Jack]

|2x(x+2)| <= |x+3|

a) pour x <= -3
x.(x+2) > 0 et donc |2x(x+2)| = 2x(x+2)
x+3 <= 0 et donc |x+3| = -x-3
et donc |2x(x+2)| <= |x+3| est équivalent à 2x(x+2) <= -x-3
Il faut donc résoudre : 2x(x+2) <= -x-3
2x² + 4x + x + 3 <= 0
2x² + 5x + 3 <= 0
(x+1)(2x+3) <= 0
tableau de signes ... : x dans [-3/2 ; -1] a l'air de convenir, mais comme on est dans le cas x <= -3 ... il n'y a pas de solutions.

b) Pour x dans ]-3 ; -2[
x.(x+2) >= 0 et donc |2x(x+2)| = 2x(x+2)
x+3 > 0 et donc |x+3| = x+3
Il faut donc résoudre : 2x(x+2) <= x+3
... sans oublier de tenir compte pour les solutions que x est dans ]-3 ; -2[

c) Pour x dans [-2 ; 0[
...

d) Pour x >= 0
...

Et finalement faire l'union de toutes les solutions trouvées dans les 4 cas.

:zen:

[chan79]

Bonjour
Une autre approche
Des nombres positifs sont rangés dans le même ordre que leurs carrés
L'inéquation équivaut à
(2x(x+2))²<=(x+3)²
(2x(x+2))²-(x+3)²<=0
(2x²+4x+x+3)(2x²+4x-x-3) <=0
(2x²+5x+3)(2x²+3x-3) <=0



Un petit tableau de signes et c'est fini
On obtient la réunion de deux intervalles

[maeee]

Pour la première équation , tu veux dire factoriser par x ?
et après étudier le signe de (-2x +10-12/x) et (x+3+2/x) ?

Merci pour toutes vos réponses!

[maeee]

Salut !



Posons .
Cherchons alors à écrire sans valeurs absolues :

Etudie, suivant les valeurs du réel , le signe de , simplifie alors ; fais-en de même avec .

Déduis-en alors, toujours suivant le réel , l'expression de et détermine enfin pour quelles valeurs de a-t-on .

Merci! Mais ne faut-il pas étudier l'inéquation lorsque la valeur absolue donne un nombre négatif ?
-2x(-x-2)<= -x -3
enfin c'est peut être un peu bête mais je n'ai jamais vraiment compris la valeur absolue :marteau:

[mrif]

Pour la question 2) je suis du même avis que chan69:
Comparer 2 nombres positifs revient à comparer leurs carrées, et cela permet de se débarrasser des valeurs absolues et de calculer proprement.

[maeee]

Pour la question 2) je suis du même avis que chan69:
Comparer 2 nombres positifs revient à comparer leurs carrées, et cela permet de se débarrasser des valeurs absolues et de calculer proprement.

Dac , merci j'ai compris
par contre pour le a) j'ai toujours pas compris

[mrif]

Dac , merci j'ai compris
par contre pour le a) j'ai toujours pas compris

Les 2 termes de la fraction sont des plynomes du second degré. Tu cherches les zéros de ces polynomes en résolvant les 2 équations:
N(x) = -2x²+10x-12 = 0 et D(x) = x²+3x+2 = 0.
Les solutions de la première sont 2 et 3 et celles de la 2 ème, -1 et -2. Donc
N(x) = -2(x-2)(x-3) et D(x) = (x+1)(x+2).

Le signe de N(x)/D(x) est celui de N(x)*D(x), signe qu'on determine en faisant un tableau de signes, sans oublier que les valeurs -1 et -2 sont interdites.
Tu obtiendras S = ]-2;-1[ U [2;3]