Espérance

[Gorosei]

Bonsoir,

Soit
1) Montrer que
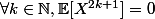
2) Montrer que

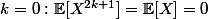
1) car
On suppose que c'est vrai au rang k, donc
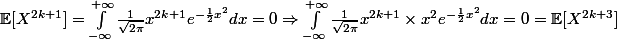
donc vrai pour tout entier naturel k

Est-ce juste ?

Pour la 2)
Après je bloque..

Merci

[Lostounet]

Salut,

On a le droit de multiplier comme ça par x^2 dans l'intégrale comme on veut ? Je ne comprends pas trop...c'est quoi ton argument ?
Tu cherches à appliquer le théorème de transfert par exemple? Tu peux.


Sinon, avez-vous vu en cours la fonction génératrice des moments ? Il y a plusieurs méthodes pour trouver les moments d'une loi normale. Tu peux chercher une relation de récurrence en utilisant des intégrations par parties aussi. Bref...

Pour les initialisations tu n'as même pas d'intégrales à calculer.
E(X^2)-(E(X))^2 = Var(X)

Donc E(X^2)=1

Avec clairement E(X)=0

[Yezu]

Salut,

Pour la 1/ il suffit de raisonner sur la parité de l'intégrant.

Pour la 2/ Supposons que qu'il existe un entier k tel que la propriété soit vraie au rang k.
Tu as donc, (je note \phi la densité de probabilité)
.
Une IPP donne :

Ce qui donne le bon résultat (il te suffit de remarquer )

EDIT : j'essaie de faire mes symboles intégrales en {\Huge ...} mais ça fait tout mon code TeX en Huge. Ça fait longtemps que je cherche le bon truc pour juste augmenter la taille des symboles int qui sont assez dégueulasses du fait de leur petitesse. Quelqu'un sait comment faire ? Sur TeXniC center que j'utilise pour mes travaux, il suffit de mettre \int dans un {\Huge} ou encore plus facilement d'utiliser l'environnement {equation} ou \[\] ...

ReEDIT : bon c'est pas si mal en fait le Huge est beaucoup plus joli que le normalsize qui est très pixélisé.

[Gorosei]

Merci pour vos réponses.

@Yezu:
1) J'utilise le raisonnement sur la parité:


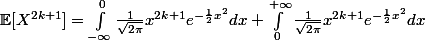
est une fonction impaire et est paire. Le produit des deux fonctions donne une fonction impaire. Donc la fonction sur est l'opposé de celle sur . Ainsi, quelque soit k un entier naturel,

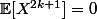
C'est mieux ?

2)Je l'ai refait et je tombe sur le même résultat, Merci !!


@Lostounet:
Nous avons rapidement vu les fonctions caractéristiques, je pense que c'est un peu pareil que les fonctions génératrice des moments ?