Bonsoir,
J ai besoin de votre aide sur comment trouver une primitive de F(x)=\int 1/((\exp x)-1) dans l intervalle ]0;+♾[
Merci.
Intégrale
9 messages
- Page 1 sur 1
Re: Intégrale
pascal16 a écrit:en multipliant en haut en bas par exp(-x), on a pas une forme u'/u ?
D accord, merci beaucoup.
Re: Intégrale
pascal16 a écrit:en multipliant en haut en bas par exp(-x), on a pas une forme u'/u ?
Je suis bloqué, je trouve intégralement de : (e-x)/((e(-x)-1)/e(x) )
et je ne sais pas comment faire.
Re: Intégrale
Salut,
pascal16 a tout dit :
F(x) = 1/(e^x - 1)
en multipliant en haut en bas par exp(-x) ...
F(x) = e^(-x)/[e^(-x).(e^x - 1)]
F(x) = e^(-x)/(1 - e^(-x))
qui, comme pascal16 l'a indiqué est de la forme u'/u

pascal16 a tout dit :
F(x) = 1/(e^x - 1)
en multipliant en haut en bas par exp(-x) ...
F(x) = e^(-x)/[e^(-x).(e^x - 1)]
F(x) = e^(-x)/(1 - e^(-x))
qui, comme pascal16 l'a indiqué est de la forme u'/u
Re: Intégrale
Black Jack a écrit:Salut,
pascal16 a tout dit :
F(x) = 1/(e^x - 1)
en multipliant en haut en bas par exp(-x) ...
F(x) = e^(-x)/[e^(-x).(e^x - 1)]
F(x) = e^(-x)/(1 - e^(-x))
qui, comme pascal16 l'a indiqué est de la forme u'/u
On a donc integrale[ln(u)]dx
Re: Intégrale
Si l'on ne voit pas cette astuce , sache que les fractions rationnelles en  se primitivent facilement en posant
se primitivent facilement en posant 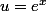 car x=ln u et donc
car x=ln u et donc 
Re: Intégrale
tournesol a écrit:Si l'on ne voit pas cette astuce , sache que les fractions rationnelles ense primitivent facilement en posant
car x=ln u et donc
J ai donc [ln|(1-e(-x)|] ?
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
