Bonjour!!!
J’ai un petit problème :
Je dois à partir d’une division euclidienne de polynômes trouver les racines de celui-ci !
Je tourne en rond depuis tout à l’heure !
Voici l’équation:
X^4-5X^2+6
A diviser par X^2-3
Ça je sais faire :
Cela fait : ( X^2+8)(X^2-3)+30
Or je dois en déduire les racines
Donc résoudre l’équation =0
J’ai essayé de factoriser ce qui me donne :
X^2(X^2 -5)+6
Sauf que là il n’y a pas de facteurs !!
Je suis bloqué là , par exemple X^2+5+6
=>X^2+11
Or la cnest impossible
Ps: Il y a probablement une ou d’autres façons de trouver les racines mais je n’en ai pas vu une en cours par conséquent j’avance à l’aveugle, je me suis probablement trompé.
Racines De Polynômes
4 messages
- Page 1 sur 1
Re: Racines De Polynômes
Salut !
Il s'agit de résoudre une équation dite "bicarrée" : pose . Cela revient à résoudre
. Cela revient à résoudre  . Or
. Or  est racine "évidente" de
est racine "évidente" de  et le produit des racines vaut
et le produit des racines vaut  donc on en conclut que l'autre racine est
donc on en conclut que l'autre racine est  (sinon, tu calcules le discriminant etc...). En conséquence
(sinon, tu calcules le discriminant etc...). En conséquence 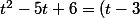(t-2)) ; ce qui, en remplaçant
; ce qui, en remplaçant  par
par  donne
donne 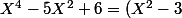(X^2-2)) .
.

Il s'agit de résoudre une équation dite "bicarrée" : pose
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Racines De Polynômes
Ok ok mercii j’ai compris!!
A l’avenir avec d’autres équations faudra que j’utilise cette méthode-ci ou tu peux avoir d’autres méthodes pour arriver au(x)résultat(s)?
A l’avenir avec d’autres équations faudra que j’utilise cette méthode-ci ou tu peux avoir d’autres méthodes pour arriver au(x)résultat(s)?
Re: Racines De Polynômes
Tu obtiens la même chose en effectuant la division euclidienne de 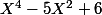 par
par 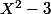 . Ce que tu as essayé de faire, mais tu as fait une erreur :
. Ce que tu as essayé de faire, mais tu as fait une erreur :
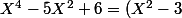X^2-2X^2+6 =(X^2-3 )X^2-2(X^2-3) = (X^2-2)(X^2-3)) .
.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
