Merci de bien vouloir m'aiderMontrer que A est une matrice antisymétrique, alors A^-1 est est une matrice antisymétrique
Preuve matrice
5 messages
- Page 1 sur 1
Preuve matrice
Bonjour, je suis entrain d'apprendre les matrice et mon professeur nous a donné une preuve a démontrer. Malheureusement je suis vraiment mauvais en pour démonstration de preuve j'aurais besoin d'aide pour la résoudre. La preuve à résoudre est ceci
Re: Preuve matrice
bonjour
vous savez que existe
existe
vous savez que
vous savez que=\left(-A\right)^t)
et donc vous savez que vous pouvez écrire le résultat général=\left(-A\right)^t=-A^t)
vous savez que^{-1}=\left(A^{-1}\right)^t)
À partir de là vous dites la phrase suivante
comme donc
donc 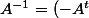^{-1}=-\left(A^t\right)^{-1}=-\left(A^{-1}\right)^t)
donc ce qu'on écrit dans les trois petits points prouvent ce qui est demandé
ce qu'on écrit dans les trois petits points prouvent ce qui est demandé
vous savez que
vous savez que
vous savez que
et donc vous savez que vous pouvez écrire le résultat général
vous savez que
À partir de là vous dites la phrase suivante
comme
donc
Re: Preuve matrice
Bonjour,
Montrer que A est une matrice antisymétrique, alors A^-1 est est une matrice antisymétrique
AT=-A <-> A est une matrice antisymétrique
((A^-1))^-1=A car -1*-1=1
=-A^-1 car A^-1=-A et -A*-1=A
donc A^-1 est antisymetrique
Montrer que A est une matrice antisymétrique, alors A^-1 est est une matrice antisymétrique
AT=-A <-> A est une matrice antisymétrique
((A^-1))^-1=A car -1*-1=1
=-A^-1 car A^-1=-A et -A*-1=A
donc A^-1 est antisymetrique
Re: Preuve matrice
bonjour
excusez moi : cette nuit dans la preuve j'ai oublié de dire (j'avais la tête ailleurs certainement) qu'il faut aussi dire que^t=A)
et comme alors
alors ^t=(-A)^t) alors
alors ^t)
puis reprendre à partir de là la derniere phrase et remplacer les trois petits points par ce qui prouve ce qui est demandé
excusez moi : cette nuit dans la preuve j'ai oublié de dire (j'avais la tête ailleurs certainement) qu'il faut aussi dire que
et comme
puis reprendre à partir de là la derniere phrase et remplacer les trois petits points par ce qui prouve ce qui est demandé
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 47 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
