changement de variable imposée
à partir de là , je n'arrive pas à m'affranchir de x
le résultat est
Une integrale
6 messages
- Page 1 sur 1
une integrale
par fibonacci » 15 Sep 2019, 17:37
bonjour,
changement de variable imposée
dx = - \left( {\frac{{x^2 + 1}}<br />{{x^2 }}} \right)dx \hfill \\<br /> dx = - \left( {\frac{{x^2 }}<br />{{x^2 + 1}}} \right)dt \hfill \\<br /> \int {\frac{{\left( {\frac{1}<br />{x} - x} \right)x}}<br />{{\left( {\frac{1}<br />{x} + x} \right)x}}} \frac{{dx}}<br />{{\sqrt {\left( {\frac{1}<br />{x} - x} \right)^2 - 2} }} = \int {\frac{{\left( {\frac{1}<br />{x} - x} \right)x}}<br />{{\left( {\frac{1}<br />{x} + x} \right)x}}} \frac{{ - x^2 dt}}<br />{{\left( {x^2 + 1} \right)\sqrt {\left( {\frac{1}<br />{x} - x} \right)^2 - 2} }} = \hfill \\ <br />\end{gathered} <br />\])
à partir de là , je n'arrive pas à m'affranchir de x
le résultat est
<br />\])
changement de variable imposée
à partir de là , je n'arrive pas à m'affranchir de x
le résultat est
Re: une integrale
par Pisigma » 15 Sep 2019, 18:01
Bonjour,
çà m'étonnerait qu'on puisse résoudre çà avec des fonctions élémentaires quand je vois la "tête" de la réponse de
Wolfram https://www.wolframalpha.com/input/?i=integrate+%281-x%5E2%29%2F%28%281%2Bx%5E2%29sqrt%281%2Bx%5E4%29%29+dx+
de plus, en rédérivant ton expression en arcsin on ne semble pas retomber sur ton énoncé
çà m'étonnerait qu'on puisse résoudre çà avec des fonctions élémentaires quand je vois la "tête" de la réponse de
Wolfram https://www.wolframalpha.com/input/?i=integrate+%281-x%5E2%29%2F%28%281%2Bx%5E2%29sqrt%281%2Bx%5E4%29%29+dx+
de plus, en rédérivant ton expression en arcsin on ne semble pas retomber sur ton énoncé
Re: une integrale
par fatal_error » 15 Sep 2019, 18:28
hi,
je sais pas, numériquement ca a l'air de coller, en modifiant up (dans [0,1]) dans le lien ci-dessous
https://repl.it/repls/ExtrasmallValidNumber
je sais pas, numériquement ca a l'air de coller, en modifiant up (dans [0,1]) dans le lien ci-dessous
https://repl.it/repls/ExtrasmallValidNumber
la vie est une fête 
Re: une integrale
par fibonacci » 16 Sep 2019, 10:41
Je vous remercie à tous les deux.
Je vais vérifier à nouveau les mises en facteur.
![:]](https://www.maths-forum.com/images/smilies/8.gif "Dan.San")
Je vais vérifier à nouveau les mises en facteur.
Re: une integrale
par GaBuZoMeu » 16 Sep 2019, 11:04
Il y a visiblement une coquille dans le "changement de variable imposé" : c'est 
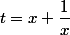
qui marche bien. Vérifie ton énoncé.
NB. Le résultat s'écrit)
.
NB. Le résultat s'écrit
Re: une integrale
par fibonacci » 16 Sep 2019, 13:26
Vraisemblablement, il y a une coquille mais je n'avais pas l'assurance pour lever le doute, pensant que mes mises en facteur était erroné. je vais regarder de plus près.
Merci
Merci
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :