Base de l’ensemble des solutions d’une equa dif

[Mathitot]

Bonjour,
Je coince sur un exercice de maths niveau prepa PC.
On a l’equation différentielle :
\frac{d^2f(t)}{dt^2}+\frac{df(t)}{dt}+f(t) =0

On nous demande de déterminer l’ensemble des fonctions de classe C2 qui vérifie l’equation.
J’obtiens quelque chose de la forme
f(t)= A exp(xt) cos(wt) + B exp(xt)sin(wt)

On nous demande ensuite de trouver une base de F l’ensemble des solutions et la je ne sais pas comment procéder.

Pouvez vous m’aider ?

[lyceen95]

Tu obtiens : f(t)= A exp(xt) cos(wt) + B exp(xt)cos(wt)
Soit tu as fait une étourderie en recopiant...
Soit tu as effectivement trouvé ça, et dans ce cas, ça se simplifie en f(t) = C exp(xt)cos(wt).

Clarifie cela, avant d'aller plus loin.

[Mathitot]

Merci pour ta réponse. C'était en effet une étourderie. J’ai corrigé ça

[Tuvasbien]

Le théorème de Cauchy-Lipschitz donne des informations sur la structure de l'ensemble des solutions.

[Mathitot]

Merci,
Mais alors avec Cauchy-Lipschitz je trouve 2 vecteurs qui génère F (l’ensemble des solutions) mais je ne sais pas quoi faire de la variable t qui est présente dans l’expression des 2vecteurs. De plus je me demandais si il était normal que l’expression de mes vecteurs de fasse en fonction d’exponentielle, de sinus et de cosinus ?

[Kolis]

Mais qui sont les ?
Tu peux difficilement donner des solutions d'une équation d'ordre 2 avec quatre nombres inconnus !

[GaBuZoMeu]

Mathitot, ce que tu sembles ne pas bien capter, c'est que les vecteurs ici sont des fonctions.
Les solutions sont des fonctions, et l'espace des solutions est un espace vectoriel de fonctions.

Ensuite, ton et ton ne sont pas n'importe quoi. Ils sont uniquement déterminés par ton équation différentielle

[Mathitot]

Oui excusez moi je me suis mal exprimé, j’ai donné le nom w et x pour ne pas encombrer +l’expression avec des valeurs numériques car ce sont des constantes.
Mais j’ai compris que les vecteurs de la base sont e^(xt) cos(wt) et e^(xt)sin(wt)
Mais ce que je ne comprends pas c’est comment déterminer la liberté de cette famille avec un terme en t. Je me demande si je peux choisir t arbitrairement pour faire une évaluation ?

[GaBuZoMeu]

Je dirais plus précisément que les vecteurs de base sont les fonctions et . Tu veux démontrer que la famille est libre pour t'assurer qu'il s'agit bien d'une base de l'espace des solutions. Comme d'hab, tu supposes qu'il existe une relation 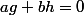avec et réels et tu essaies de montrer que 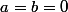. La relation 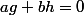veut dire que pour tout réel on a . Tu peux donc prendre des bien choisis pour arriver à tes fins.

[Mathitot]

Merci beaucoup pour ta réponse très complète. Je pense que c’est surtout le fait de manipuler des fonctions et mon manque de rigueur qui m’a porté défaut pour ce problème. Je vais essayer d’être plus rigoureux à la venir.

[GaBuZoMeu]

Ce n'est pas évident de se dire que les éléments d'un espace vectoriel peuvent être des fonctions, des polynômes, des matrices, ... tout un tas de choses. Et ça se manifeste par des difficultés quand il s'agit d'appliquer les concepts d'algèbre linéaire à ce type d'objets. Mais ça vient avec l'expérience, et je pense que tu es sur la bonne voie.