Comme prévu, l'individu imaginaire n'a pas compris grand chose à la démonstration.Il s'est tout de même aperçu que la démonstration n'est pas complète (bon, je le disais explicitement, donc pas besoin d'être très malin pour s'en apercevoir).
PS. Il est clair que la partie importante de la démonstration de GBZM est absente. Je la soupçonne d'utiliser les étapes de l'établissement de la variance et de la démonstration de la loi des grands nombres. Enfin, c'est pas grave.
Et bien sûr, un commentaire qui n'a rien à voir avec la choucroute. La loi des grands nombres !!!


Ce qui manque, c'est juste la vérification que, pour

, on a
^2})
À la demande générale

, j'en fais une démonstration basique "visuelle", puisqu'on est dans la section lycée.
On commence par quelque chose de bien connu :

On peut visualiser comme ça :
\times(1+q+q^2+q^3+\cdots)&=&1&+&q&+&q^2&+& q^3+\cdots\\ &&&-&q&-&q^2&-& q^3-\cdots\\ &= &1&&&&&&\end{array})
et justifier en parlant de la somme des termes d'une progression géométrique. Une fois ceci établi, on passe à
^2}&=(1+q+q^2+q^3+\cdots)\times (1+q+q^2+q^3+\cdots)\\ &=1+q+q^2+q^3+\cdots\\ &\phantom{=1}{}+q+q^2+q^3+\cdots\\&\phantom{=1+q}{}+q^2+q^3+\cdots\\&\phantom{=1+q+q^2}{}+q^3+\cdots\\&\phantom{=1+q+q^2+q^3}{}+\cdots\\&\\&=1+2q+3q^2+4q^3+\cdots = \sum_{k=1}^{\infty} k\,q^{k-1}\end{array})
On peut justifier ici aussi, en passant par des sommes partielles.
Bon, je m'arrête ici et je laisse à Beagle le soin d'essayer de raisonner notre individu imaginaire. C'est à mon avis (basé sur une longue expérience) peine perdue. Reconnaître qu'on se trompe depuis de si nombreuses années, c'est moins confortable que de continuer de penser qu'on a raison contre tout le monde et contre toute démarche scientifique, et notre individu imaginaire ne le fera jamais..
Récapitulons la discussion sur les commentaires de notre individu imaginaire : la loi géométrique de paramètre
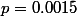
donne une espérance de

. C'est un théorème mathématique, j'en ai redonné la démonstration. Toute simulation faite par n'importe qui n'importe où dans n'importe quel logiciel sérieux confirme ce fait en donnant une moyenne proche de 667. Même notre personnage imaginaire trouve ceci quand il fait la simulation avec un générateur de nombres pseudo-aléatoires sérieux, utilisé par toute la communauté scientifique pour faire des simulations courantes.
Mais notre personnage imaginaire trouve une moyenne de 545 quand il fait la simulation avec un générateur mystère (de son cru ?). Côté mathématique, absolument aucun argument pour justifier cette moyenne (normal, elle est injustifiable). Conclusion : le générateur est complètement foireux. On ne peut accorder absolument aucun crédit à une simulation faite par notre personnage imaginaire, il en a lui-même apporté la preuve éclatante.

