Exercice fonction

[benni]

Bonjour,
J'ai un exercice que je ne comprends pas du tout. J'espère que vous pourrez m'aider :

On donne f(x)= - x (au carré)+7x
1) Donner les coordonnées du point d'intersection de la courbe avec l'axe des ordonnées.
2) Donner les coordonnées des points d'intersection de la courbe avec l'axe des abscisses.
3) Montrer que la courbe représentative de f est symétrique par rapport à la droite verticale d'équation x= 7/2

merci beaucoup

[aymanemaysae]

Bonjour;


1)

La courbe coupe l'axe des ordonnées au point de coordonnées .

[benni]

Pouvez-vous me l'expliquer plus précisément ?
Merci

[laetidom]

Pouvez-vous me l'expliquer plus précisément ?
Merci

Bonjour,
1) Comment tu écris l'équation de l'axe des ordonnées ?
Tous les points qui sont sur cet axe ont quelle abscisse ? ===> x= . . . ? (c'est ça son équation)
Ensuite, si tu veux l'intersection avec la courbe, et bien, tu te dis, si je mets l'abscisse trouvée de mon axe "dans" l'équation de la courbe, j'obtiendrais l'ordonnée du point d'intersection, non ? . . . Essaye et dis-nous ! :
y = f( . . . ? ) = . . . ?

Donc le point cherché aura pour coordonnées ( . . . ? ; . . . ?)

[aymanemaysae]

Dans un repère orthonormé , si une courbe coupe l'axe des ordonnées , alors elle le coupe au point d'abscisse 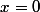et bien sûr d'ordonnée : ce point si il existe , il est unique et c'est le point de coordonnées : dans ton exercice , tu as , donc coupe l'axe des ordonnées au point de coordonnées qui est l'origine du repère orthonormé .

On doit remarquer que coupe l'axe des abscisses aux points d'ordonnée 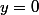, c - à - d aux points de coordonnées , c - à - d dont les abscisses vérifient : .

A toi maintenant de résoudre l'équation : .

[benni]

Quand une courbe coupe un axe ça donne 0 tout le temps ?

[aymanemaysae]

La réponse est non : Si la courbe coupe l'axe des ordonnées , l'abscisse du point d'intersection est : x = 0 ;
donc pour déterminer le point d'intersection , on doit calculer : f(0) qui est l'ordonnée du point , donc enfin
on a les coordonnées du point qui sont : (0 ; f(0)) ,et s i la courbe coupe l'axe des abscisses , les ordonnées des points d'intersection sont : y = 0 ; donc pour avoir leur abscisses , on doit résoudre l'équation : f(x) = 0 .

La courbe coupe l'axe des ordonnées au point de coordonnées (0 ; f(0)) , et comme f(0) = - 0² + 7 * 0 = 0 ;
donc les coordonnées en question sont : (0 ; 0) qui sont les coordonnées de l'origine du repère orthonormé .

La courbe coupe l'axe des abscisses , aux points d'abscisses x vérifiant : f(x) = 0 ; donc : - x² + 7x = 0 ;
donc : x(-x + 7) = 0 ; donc : x = 0 ou - x + 7 = 0 ; donc : x = 0 ou x = 7 ; donc les points où la courbe coupe l'axe
des abscisses ont respectivement pour coordonnées : (0 ; 0) et (7 ; 0) qui sont les points A et B de la figure .