bonjour à tous; svp j'ai commencé à faire un exercice mais je bloque a niveau. merci d'avance de votre aide
enonce:
soit f une fonction definie de R vers R; 2pi periodique , f(x)= e^x sur ]-pi; pi]
1- calculer les coefficients de fourier exponentiels de f
2- etudier la convergence ( simple, uniforme) de la serie
3- calculer les sommes suivantes
Serie de fourier
8 messages
- Page 1 sur 1
Re: serie de fourier
Bonjour,
je connais les coefficients de Fourier, mais les coefficients de Fourier exponentiels, jamais entendu parler... ça existe, ce machin là ?
je connais les coefficients de Fourier, mais les coefficients de Fourier exponentiels, jamais entendu parler... ça existe, ce machin là ?
Re: serie de fourier
Bonjour
Oui ça existe . Pour la période la base orthogonale est
la base orthogonale est _{n \in \Z})

Pour qu'elle soit orthonormée le produit scalaire est :
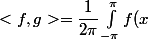\bar{g(x)} dx)
La facteur est facile à retrouver en calculant
est facile à retrouver en calculant 
La correspondance de cette b.o.n de Fourier avec la base trigo est donnée grâce à
=cos( n\pi .)) et
et (e_n- e_n)=sin( n\pi.))
Oui ça existe . Pour la période
Pour qu'elle soit orthonormée le produit scalaire est :
La facteur
La correspondance de cette b.o.n de Fourier avec la base trigo est donnée grâce à
Re: serie de fourier
ah! je connaissais! mais je les appelle les coefficients de Fourier complexes! merci pour la clarification
Re: serie de fourier
est ce que vous pourriez m'aider a calculer les coefficients de fourier et etudier la convergence? svp
Re: serie de fourier
MAV a écrit:est ce que vous pourriez m'aider a calculer les coefficients de fourier et etudier la convergence? svp
Salut,
Tu as dans ton cours une formule pour calculer
Sinon, tu dois avoir dans ton cours des formules pour calculer
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: serie de fourier
Bonjour
Bon je peux donner une indication supplémentaire de @lostounet si=e^x) sur
sur )
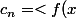, e^{inx}>) c'est à dire que ça va être une intégrale sous la forme d'une exponentielle donc facile à calculer. (au passage ça me fait penser que c'est une bonne raison de passer par là avant d'écrire la serei en cos et sin)
c'est à dire que ça va être une intégrale sous la forme d'une exponentielle donc facile à calculer. (au passage ça me fait penser que c'est une bonne raison de passer par là avant d'écrire la serei en cos et sin)
Pour) et
et ) tu peux utiliser les formules de cours mais tu peux grâce à la réponse que j'ai donnée à LB2
tu peux utiliser les formules de cours mais tu peux grâce à la réponse que j'ai donnée à LB2
directement à partir des)
Bon je peux donner une indication supplémentaire de @lostounet si
Pour
directement à partir des
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 111 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
