Merci d'avance.
Calcul d'integrale
16 messages
- Page 1 sur 1
Calcul d'integrale
Bonjour, je suis désolé de vous embéter mais j'ai besoin d'aide pour calculer cetta integrale. Je pense pas que cela doit etre compliqué mais je séche et c'est trés frustrant... voici la bete :
^2d\theta}{a-b\cos(\theta)}})
Merci d'avance.
Merci d'avance.
tize a écrit:Je viens d'essayer... je tombe sur :(sauf erreur de calculs, tu peux confirmer ?) mais ça n'est pas beaucoup plus réjouissant...
[edit] : il n'y aurait pas une condition sur a et b ?
Bon ben en fait ce que tu trouve c'est l'integrale originale. En fait j'avais déja fait le changement de variable
... Mon intuition me dit que l'on est sur la bonne voit avec ce changement de variable mais je séche .... Merci a toi quand meme.\tetha=2\cos(t)
maturin a écrit:moi je pense qu'au contraire c'est compliqué comme intégrale.
sinon comme condition on doit avoir |a|>=|b| pour que ce soit intégrable.
tu le tires d'un exercice ton truc ? Genre t'es sûr qu'il y a une solution simple ?
Je suis sur qu'il y a une solution car je le tire d'un bouquin de physique sur les verre de spin mais y a pa le détaille de calcul et j'ai besoin du résultat de l'integration pour résoudre un autre problème mais qui a une formulation similaire. Aprés je ne sais pas si la solution est simple.... Merci a vous quand meme d'essaiyer...
Je crois que les règles de Bioche s'appliquent pas et qu'il faut aller au charbon en ) .
.
J'obtiens comme intégrande :
(t^2+k)}) , où k=(a+b)/(a-b).
, où k=(a+b)/(a-b).
Il reste à décomposer en éléments simples en écrivant que le numérateur de la deuxième fraction est (t²+k)-(t²+1) une constante multiplicative près.
Je laisse ctouya vérifier et finir.
J'obtiens comme intégrande :
Il reste à décomposer en éléments simples en écrivant que le numérateur de la deuxième fraction est (t²+k)-(t²+1) une constante multiplicative près.
Je laisse ctouya vérifier et finir.
yos a écrit:Je crois que les règles de Bioche s'appliquent pas et qu'il faut aller au charbon en.
J'obtiens comme intégrande :, où k=(a+b)/(a-b).
Il reste à décomposer en éléments simples en écrivant que le numérateur de la deuxième fraction est (t²+k)-(t²+1) une constante multiplicative près.
Je laisse ctouya vérifier et finir.
Merci, je me lance. J'avais obtenue le résultat avec mathematica mais ce n'était pas satisfaisant je vous tien donc au courant.
les bornes
yos a écrit:Oui en effet!
J'obtiens :.
Et comme décomposition (à vérifier et sous réserve que k>0) :.
Le terme central s'intègre par parties.
Rebonjours a tous. Je veux pas vous embéter plus que je ne l'ai déjà fait mais quelles sont les borne d'integration? Car j'ai l'impression que l'integration par partie diverge :hum: et c'est pas cool sa... Sinon j'ai pas de condition spéciale pour a et b en fait c'est des paramétre d'une fonction que j'essaye de minimizer (un peut comme des multiplicateur de Lagrange).
Bonjour,
Une autre façon de faire pour éviter ce problème :
d\theta=\int_0^{\pi/2}\;f(\theta)d\theta+\int_{\pi/2}^{\pi}\;f(\theta)d\theta)
Dans la deuxième intégrale, on fait le changement de variable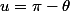 qui donne en remarquant que
qui donne en remarquant que =-cos(\theta)) et
et =sin(\theta))
}{a-bcos(u)}du+\int_0^{\pi/2}\;\frac{sin^2(u)}{a+bcos(u)}du)
(j'ai remplacé le theta par u dans la première intégrale)
On peut donc regrouper et effectuer les calculs :}{a^2-b^2cos^2(u)}du=\int_0^{\pi/2}\;\frac{2adu}{b^2}+\int_0^{\pi/2}\;\frac{2a (b^2-a^2)}{b^2(a^2-b^2cos^2(u))}du)
On peut alors poser t=tan(u)
dt}{ab^2(t^2+k)})
avec k=1-(b/a)²
Les solutions sont alors des log ou des arc tg selon le signe de k
k positif->}{b^2})
si k est négatif, il y a un problème
Avec sans doute quelques erreurs de calcul :we:
Une autre façon de faire pour éviter ce problème :
Dans la deuxième intégrale, on fait le changement de variable
(j'ai remplacé le theta par u dans la première intégrale)
On peut donc regrouper et effectuer les calculs :
On peut alors poser t=tan(u)
avec k=1-(b/a)²
Les solutions sont alors des log ou des arc tg selon le signe de k
k positif->
si k est négatif, il y a un problème
Avec sans doute quelques erreurs de calcul :we:
alben a écrit:Bonjour,
Une autre façon de faire pour éviter ce problème :
Dans la deuxième intégrale, on fait le changement de variablequi donne en remarquant que
et
(j'ai remplacé le theta par u dans la première intégrale)
On peut donc regrouper et effectuer les calculs :
On peut alors poser t=tan(u)
avec k=1-(b/a)²
Les solutions sont alors des log ou des arc tg selon le signe de k
k positif->
si k est négatif, il y a un problème
Avec sans doute quelques erreurs de calcul :we:
Merci a toi Alben grace a toi j'ai pu résoudre mon problème de maniere élégante je te remercie vraiment ainsi que les autres menbres de ce forum qui mon aidé. Bref Merci
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 31 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
