Bonjour, j'aurais voulu savoir si c'était possible d'avoir un tableau de variation sans valeurs correspondant aux images dans celui-ci.
Voici l'énoncé de mon exercice:
Soit f une fonction vérifiant:
•f est définie sur [-10;10]
•f est croissante sur [-4;0] et sur [5;10] puis f est décroissante dur [-10;-4] et sur [0;5]
•les antécédents par f de 0 sont -2;2 et 10
• le minimum de f sur [-10:10] est -2 puis le maximum de f sur [-10;10] est 5
• f(1)=3
• la représentation graphique de f coupel'axe des ordonnées 4.
1) Dresser le tableau de variation de f
2) Comparer f(-5) et f(-8) puis comparer f(1) et f(7)
3) Construire, dans un repère, une courbe susceptible de représenter f.
4) Donner le meilleur encadrement possible de f(x) quand [x]appartient[-4;5].
Merci d'avance pour vos réponses.
Tableau de variation
13 messages
- Page 1 sur 1
Re: Tableau de variation
Où est le problème ?
Peux tu nous dire ce que tu as déjà réussi à inscrire dans ton tableau de variation ?
Peux tu nous dire ce que tu as déjà réussi à inscrire dans ton tableau de variation ?
Re: Tableau de variation
Oui, en réalité mon tableau de variation est fait mais j'ai un doute puisque je n'ai pas de valeurs dans la partie des images, au bout et au début des flèche en fait.
Re: Tableau de variation
Donc f(10)=0Cloclo812 a écrit:•f est croissante sur [-4;0] et sur [5;10] puis f est décroissante dur [-10;-4] et sur [0;5]
•les antécédents par f de 0 sont -2;2 et 10
On peut aussi ajouter les valeurs -2 et 2 de x qui ont pour image 0
Donc f(0)=4• la représentation graphique de f coupel'axe des ordonnées 4.
Donc f(-10)=5• le minimum de f sur [-10:10] est -2 puis le maximum de f sur [-10;10] est 5
Par contre on n'a pas suffisamment de données pour savoir si c'est f(-4) ou f(5) qui vaut -2.
On peut aussi ajouter la valeur :
• f(1)=3
Re: Tableau de variation
Bonjour, je dois réaliser le meilleur encadrement de f(x) lorsque celui ci appartient à [-4 ; 5] mais je ne sais pas comment m'y prendre
Re: Tableau de variation
f est croissante sur [-4;0] puis f est décroissante sur [0;5]
les variations de f te disent que tu as un maximum (local) en x=0 qui vaut f(0)
comme f(1)=3, on sait juste que f(0) >= 3 car il doit être plus grand que f(1)
le minimum, c'est soit f(-4), soit f(5)
or ton tableau de variations te dit que le minimum sur [-10;10] est lui aussi soit f(-4) soit f(5), et " le minimum de f sur [-10:10] est -2 ", donc -2 est le minimum sur [-4;5]
les variations de f te disent que tu as un maximum (local) en x=0 qui vaut f(0)
comme f(1)=3, on sait juste que f(0) >= 3 car il doit être plus grand que f(1)
le minimum, c'est soit f(-4), soit f(5)
or ton tableau de variations te dit que le minimum sur [-10;10] est lui aussi soit f(-4) soit f(5), et " le minimum de f sur [-10:10] est -2 ", donc -2 est le minimum sur [-4;5]
Re: Tableau de variation
As-tu fait le tableau de variations ?
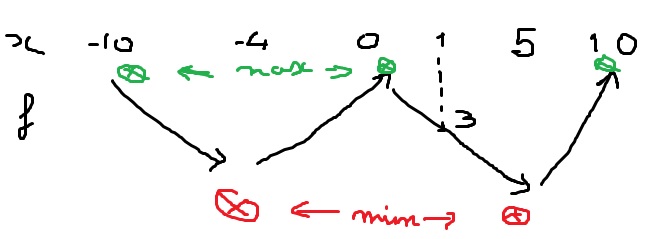
en rouge : les seuls endroits où f peut atteindre un minimum
en verte : là où elle peut atteindre un maximum

en rouge : les seuls endroits où f peut atteindre un minimum
en verte : là où elle peut atteindre un maximum
Re: Tableau de variation
Oui, je l'ai fait mais je n'ai pas penser comme cela mais c'est vrai maintenant ça paraît logique merci !
Re: Tableau de variation
pascal16 a écrit:As-tu fait le tableau de variations ?
en rouge : les seuls endroits où f peut atteindre un minimum
en verte : là où elle peut atteindre un maximum
Donc si je comprend bien -2<f(x)<0
Re: Tableau de variation
sur [-4;5], on a -2<f(x)<f(0)
si on place en plus les antécédents de 0, on a que f(-1) doit être négatif si on ne veut que 3 solutions pour f(x)=0
du coup f(10)=0
finalement le maximum de f ne peu être atteint que pour x=0, vaut f(0) mais vaut aussi 5 d'apès l'énoncé.
f(0)=5
si on place en plus les antécédents de 0, on a que f(-1) doit être négatif si on ne veut que 3 solutions pour f(x)=0
du coup f(10)=0
finalement le maximum de f ne peu être atteint que pour x=0, vaut f(0) mais vaut aussi 5 d'apès l'énoncé.
f(0)=5
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
