Probabilité de retrouver deux fois le même mot parmi une lis

[jj76]

Bonjour,
J'ai un mot de 36 caractères UNICODE (chaque caractère pouvant avoir 2 exposant 16 valeurs différentes)
sauriez vous combien j'ai combien de chance d'avoir 2 fois la même séquences de 36 caractères, dans un jeux de 200 000 mot de 36 caractères de ces caractères?
et pour 1 million de mots ?
Merci d'avance.

[Ben314]

Salut,
Des suites (=mots) quelconques de 36 symboles appartenant chacun à un ensemble de cardinal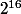 , il y en a .
Ensuite, si tu tire au hasard (et de façon indépendante) tels mots, il y a tirages possible mais seulement où tout les mots tirés sont différents (le deuxième mot tiré doit être différent du premier ; le troisième mot tiré doit être différent des deux premiers ; etc...).
Il y a donc une proba que tout les mots tirés soient différents.
De plus, si est bien plus petit que , alors donc si 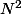est bien plus petit que .

Bref, ici, avec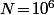 et 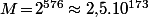, la proba. de tirer autre chose que des mots tous différents est de l'ordre de . . .
Et pour que la proba soit autre chose que "quasi" 0, ben il faudrait tirer un nombre de mot de l'ordre de donc de l'ordre de mots (et si tu tire un milliard de mots toute les millisecondes, ça demanderais juste 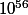fois plus de temps que celui écoulé depuis le Big Bang)

[jj76]

Merci et pour 36 symboles appartenant chacun à un ensemble de cardinal , de 2 exposant 8 au lieu de 16 ?