Bonsoir,
J'ai besoin d'aide pour cet exo, merci en avance.
Dans un parallélogramme ABCD, on considère les points M, N et P tels que:
AM=3/4 AB , CN=2/3CB ET DP=1/2 DC
Démontrer que les droites (MD) et (PN) sont parallèles.
P.s : je sais pas comment mettre les flèches sur les vecteurs.
Exo sur les vecteurs
6 messages
- Page 1 sur 1
Re: Exo sur les vecteurs
tu peux exprimer les vecteurs MD et PN en fonction de AB et AD et utilisant ce qui t'es donné et les égalités de vecteurs dans le parallélogramme
Re: Exo sur les vecteurs
Salut,
Une autre manière (plus simple) de le démontrer, est de montrer que les triangles AMD et CPN sont semblables
Une autre manière (plus simple) de le démontrer, est de montrer que les triangles AMD et CPN sont semblables
Re: Exo sur les vecteurs
Bonjour;
ABCD est un parallélogramme , donc :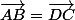 et
et 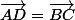 .
.
On a :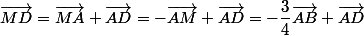 .
.
On a aussi :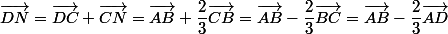 ;
;
donc :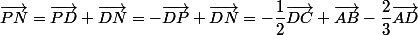
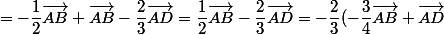 = - \dfrac{2}{3} \vec{MD}) .
.
Conclusion :
On a :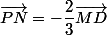 donc les droites
donc les droites ) et
et ) sont parallèles .
sont parallèles .
Pour t'exercer un peu , tu peux essayer de résoudre cet exercice en suivant les autres démarches proposées .
ABCD est un parallélogramme , donc :
On a :
On a aussi :
donc :
Conclusion :
On a :
Pour t'exercer un peu , tu peux essayer de résoudre cet exercice en suivant les autres démarches proposées .
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
