Bonjour à tous je suis en train de refaire des exercises sur la convexité mais je Rien comprendre malgré la correction que j'avais prise inconsciemment en cours, voici l'exercice :
F défini sur [-4; 4] par f (x) 1/2 × X2 + 3/4 - 1 , avec le graphique qui va à côté et la tengeante d'abscisse 2 , ( f est convexe tout le long )
Il est donc demander de déduire que pour tout X [ 4;4] , 1/2 × X2 + 3/4 - 1 sup ou égale à 11/4 X - 3 , il faut apparemment utiliser la formule f'(a) ( x- a ) + f (2) mais ensuite ??
Merci d'avance de votre aide
Exercise convexité
6 messages
- Page 1 sur 1
Re: Exercise convexité
Bonjour;
Tu as : = \dfrac{1}{2}x^2+\dfrac{3}{4}x-1)
D'après le graphique , la tangente passe par les points de coordonnées (0 ; - 3) et (4 ; 8) ;
donc le coefficient directeur de la tangente à
de la tangente à  (la courbe représentative de
(la courbe représentative de  )
)
au point d'abscisse est :
est : }{4 - 0} = \dfrac{11}{4}) , et son ordonnée à l'origine
, et son ordonnée à l'origine  est :
est : 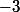 ;
;
donc l'équation réduite de la tangente est : = ........................ .
= ........................ .
Tu peux conclure maintenant .

Tu as :
D'après le graphique , la tangente passe par les points de coordonnées (0 ; - 3) et (4 ; 8) ;
donc le coefficient directeur
au point d'abscisse
donc l'équation réduite de la tangente est :
Tu peux conclure maintenant .

Re: Exercise convexité
bjr,
la fonction f est strictement convexe sur car de dérivée seconde positive.
car de dérivée seconde positive.
=1 > 0)
on en conclut que la courbe de f est située au dessus de ses tangentes.
en particulier, en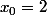
 \geq \dfrac{11}{4}x-3)
Autre méthode
\geq \dfrac{11}{4}x-3 \Leftrightarrow \frac{1}{2} (x-2)^2 \geq 0)
la fonction f est strictement convexe sur
on en conclut que la courbe de f est située au dessus de ses tangentes.
en particulier, en
Autre méthode
Re: Exercise convexité
Bonsoir merci beaucoup à vous deux ! je n'avais pas fais le lien avec le coef directeur et profité du fait que f(x) est tout le temps convexe , du coup j'ai finalement réussi l'exercise mais je rebloque à nouveau sur le suivant, j'en profite d'être ici pour ne pas ouvrir un nouveau sujet :
C (x) = 0,05x^3 - 1,05x^2+8x+4
1 ) Evaluer la convexité de la fonction à l'aide de la calculatrice ( fais ) ...
2) Démontrer ces résultats ... C'est à dire ? J'ai beau chercher mais n'ayant pas de questions du même genre je sèche et ne trouve rien , puis 3 ) Interpréter les résultats , que je comprends encore moins mais je le ferai après .
Merci d'avance , et si vous auriez un lien à partager depuis youtube traitant de mon problème , n'hésiter pas à le faire, car je n'ai rien trouvé
C (x) = 0,05x^3 - 1,05x^2+8x+4
1 ) Evaluer la convexité de la fonction à l'aide de la calculatrice ( fais ) ...
2) Démontrer ces résultats ... C'est à dire ? J'ai beau chercher mais n'ayant pas de questions du même genre je sèche et ne trouve rien , puis 3 ) Interpréter les résultats , que je comprends encore moins mais je le ferai après .
Merci d'avance , et si vous auriez un lien à partager depuis youtube traitant de mon problème , n'hésiter pas à le faire, car je n'ai rien trouvé
Re: Exercise convexité
bonjour,
calcule la dérive seconde de f (i.e f''). Sur quels intervalles est elle positive ?
calcule la dérive seconde de f (i.e f''). Sur quels intervalles est elle positive ?
Re: Exercise convexité
D'accord , j'ai donc essayé de calculer en premier la dérivé de C(x) le seul problème est que dès que je rentre X dans n'importe quel calcul , ma calculatrice n'affiche pas le bon résultat , je fais par exemple 2 x 2X et elle affiche 28,7 ?? Au lieu de 4X ..
Il y a t-il un moyen de réinitialiser la calculatrice ou bien faut il être dans un mode particulier ? Voilà après cette question je ne vous embête plus
Il y a t-il un moyen de réinitialiser la calculatrice ou bien faut il être dans un mode particulier ? Voilà après cette question je ne vous embête plus
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 170 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
