Primitive de (1-exp(ax))
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
dalinda
- Messages: 5
- Enregistré le: 10 Sep 2018, 12:44
-
 par dalinda » 26 Nov 2018, 17:39
par dalinda » 26 Nov 2018, 17:39
Bonjour,
Je suis en train de chercher une primitive de la fonction
 = \bigg [1- exp \left(\frac{{ cste } }{ 1+x^2}\right ) \bigg])
et on sait que
 dx=\left(\frac{{ 1} }{ a}\right )*exp(ax))
mais j'ai encore des difficultés pour la résoudre avec un changement de variable.
Avez vous une idéé ?
Cordialement

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 26 Nov 2018, 17:51
par Ben314 » 26 Nov 2018, 17:51
Salut,
J'ai plus que de gros doute concernant le fait qu'on puisse exprimer à l'aide des fonctions usuelles une primitive de
)
.
Et ça n'a évidement pas le moindre rapport avec une fonction du type
)
avec

constant.
Tu es sensé en faire quoi de tes primitives ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
dalinda
- Messages: 5
- Enregistré le: 10 Sep 2018, 12:44
-
 par dalinda » 29 Nov 2018, 11:56
par dalinda » 29 Nov 2018, 11:56
@Ben314
je veux calculer cette fonction
 \bigg] dx)
pour pouvoir l’utiliser après dans un autre problème

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 30 Nov 2018, 13:12
par Ben314 » 30 Nov 2018, 13:12
Sauf erreur,
=\int_0^{+\infty}\left[1-\exp\big(\frac{c}{1+x^2}\big)\right]dx<br />= -\sum_{n\geq 1}\dfrac{c^n}{n!}\int_0^{+\infty}\!\!\!\dfrac{dx}{(1\!+\!x^2)^n}<br />= -\sum_{n\geq 1}\dfrac{c^n}{n!}\!\times\!\dfrac{(2n-2)!\,\pi}{2^{2n-1}(n-1)!^2}<br />=-2\pi G\big(\frac{c}{4}\big))
\!=\!\sum_{n\geq\! 1}a_n x^n\ \text{ avec }\ a_n\!=\!\dfrac{(2n\!- \!2)!}{(n\!-\!1)!^2\!\times\!n!}\text{ et le fait que }a_{n+1}\!=\!\dfrac{4n-2}{n(n\!+ \!1)}\text{ permet de montrer que })
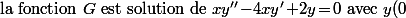\!=\!0\text{ et }y'(0)\!=\!1})
.
Et là, on tombe assez vite sur les
fonctions de Bessel relativement connues.
Modifié en dernier par
Ben314 le 02 Déc 2018, 11:24, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
dalinda
- Messages: 5
- Enregistré le: 10 Sep 2018, 12:44
-
 par dalinda » 02 Déc 2018, 10:45
par dalinda » 02 Déc 2018, 10:45
@Ben314 merci pour votre réponse
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités